1.前、后两车轮输入的功率谱密度与互谱密度
上面只讨论了一个车轮的自功率谱,如果考虑前、后车轮两个输入时,还要研究两个输入之间的互功率谱问题。如图3-3所示,x(I)为前轮遇到的不平度函数,假定前、后轮走同一个车辙,则后轮只是比前轮滞后一段长度I(轴距),因而后轮不平度函数为x(I-l)。
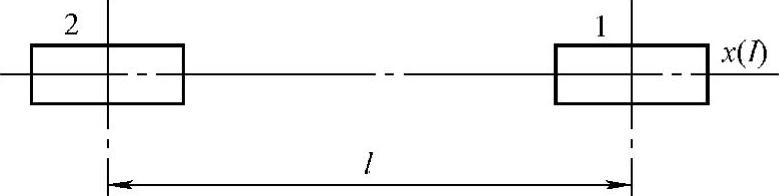
图3-3 前、后车轮的两个输入
如令x(I)的傅里叶变换为X(n),即
F[x(I)]=X(n) (3-14)
则根据傅里叶变换的性质可得
F[x(I-l)]=X(n)e-j2πnl (3-15)
如果激励前、后轮的道路谱的自谱、互谱分别用G11(n)、G22(n)、G12(n)和G21(n)表示,则有


式中,L为路面长度I方向上的分析距离,X*(n)为X(n)的共轭复数。以上各式也可以写成矩阵形式,即
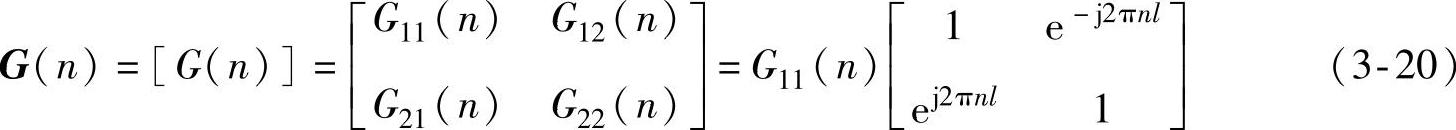
写成时间频率的功率谱则为

2.四轮输入时的功率谱密度与互谱密度
图3-4所示为四轮输入示意图。四车轮输入时,如果x(I)、y(I)分别为左前轮和右前轮遇到的不平度函数,则左后轮和右后轮不平度函数分别为x(I-l)、y(I-l)。(https://www.xing528.com)
根据不平度函数的傅里叶变换与功率谱之间关系,可得四个车轮输入的自功率谱和四个车轮彼此间输入的互功率谱,共16个谱量Gik(n)(i,k=1,2,3,4),为

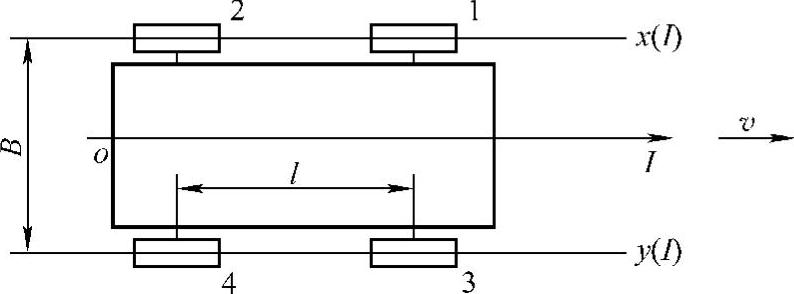
图3-4 四轮输入示意图
因此,四个车轮输入的自功率谱和互功率谱,共16个谱量分别为

两个轮迹之间不平度的统计特性,用它们之间的互功率谱密度函数或相干函数来描述。互谱密度一般为复数,用指数形式表示时,左、右轮迹间的互谱可以表示为

式中,Gxy(n)为x(I)与y(I)的互振幅功率谱;ϕxy(n)为x(I)与y(I)的互相位谱。
两个轮迹的相干函数,可表示为

相干函数coh2xy(n)在频域内描述了x(I)与y(I)中频率为n的分量之间线性相关的程度。当coh2xy(n)=1时,表明对x(I)与y(I)中频率为n的分量之间幅值比和相位差保持不变,即完全线性相关;当coh2xy(n)=0时,表明x(I)与y(I)中频率为n的分量之间幅值比和相位差是完全无关地随机变化的。
当两个轮迹x(I)与y(I)的统计特性相同,即Gxx(n)=Gyy(n)=Gq(n),且相位差在ϕxy(n)=0时,由式(3-25)可得
Gxy(n)=Gyx(n)=cohxy(n)Gq(n) (3-26)
路面对四轮汽车输入的谱矩阵可以表示为
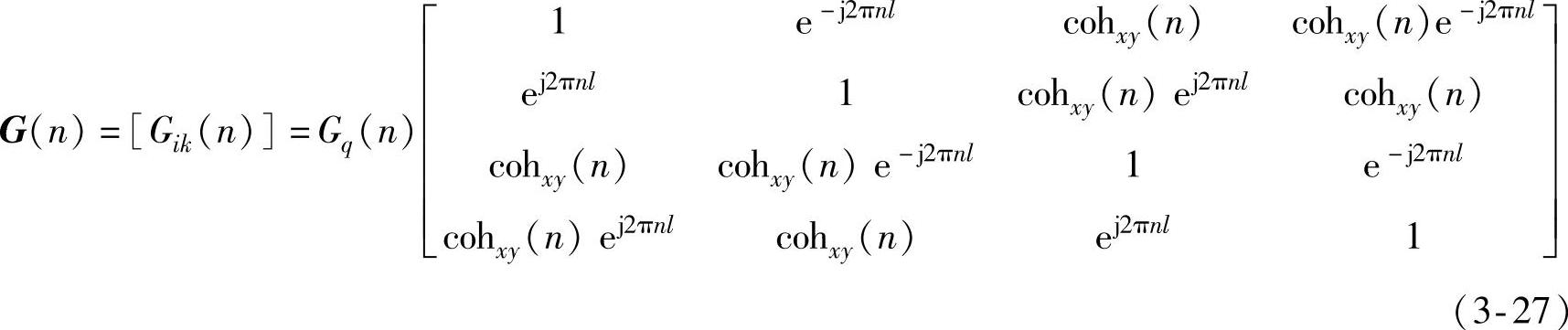
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




