双质量无阻尼系统自由振动的设计与仿真

当系统可以不计阻尼时，则双质量系统的自由振动微分方程变为

由运动方程可以看出，m₂与m₁的振动是相互耦合的。若m₁不动（z₁=0），则有

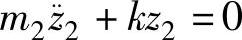
这相当于只有车身质量m₂的单质量无阻尼自由振动。其固有圆频率为

同样，若m₂不动（z₂=0），相当于车轮质量m₁作单自由度无阻尼自由振动，于是可得

车轮部分固有圆频率为

固有圆频率p₀与p_t是只有单独一个质量（车身质量或车辆质量）振动时的部分频率，称为偏频。

在无阻尼自由振动时，车身质量和车轮质量将以相同的圆频率ω和相角φ作简谐振动，设车轮和车身的振幅分别为z₁₀和z₂₀，则它们的振动响应分别为

将式（2-54）和式（2-55）代入振动微分方程组（2-51），可得

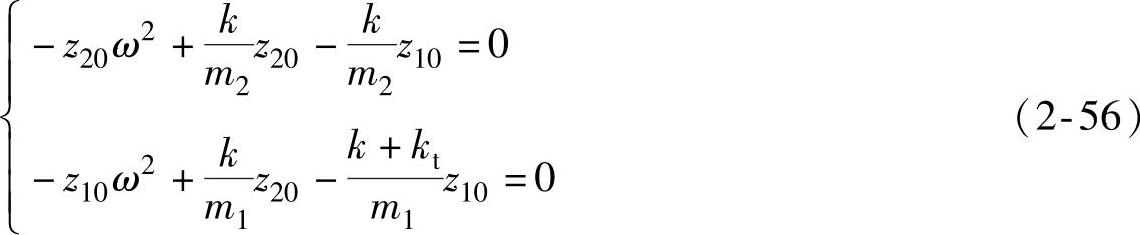
将k/m₂=p²₀、（k+k_t）/m₁=p²_t代入式（2-56），可得

此方程组有非零解的条件是z₂₀、z₁₀的系数行列式为零，即

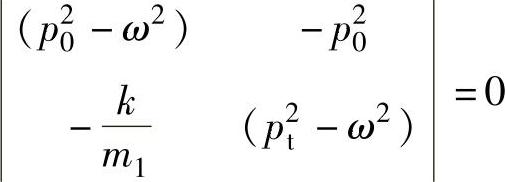
得系统的特征方程为

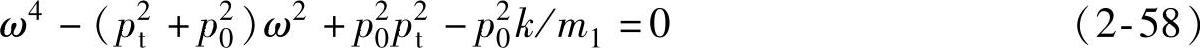
方程（2-58）的两个根为二自由度系统的两个主频率ω₁和ω₂的平方

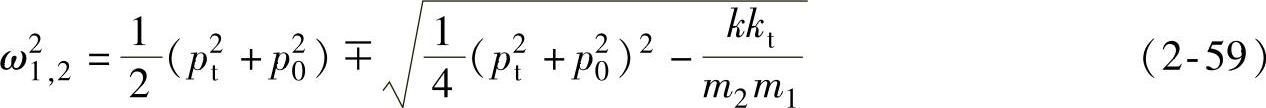
将ω₁和ω₂代入式（2-57）中的任何一式，可得一阶主振型和二阶主振型，即

一阶主振型：

二阶主振型：(www.xing528.com)

例如，某汽车车身固有圆频率p₀=2πrad/s，质量比r_m=m₂/m₁=10，刚度比r_k=k_t/k=9，求系统的主频率和主振型。

由式（2-53）可得车轮的固有频率为

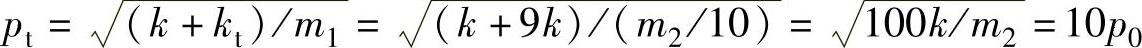
由式（2-59）可得系统两个主频率分别为

ω₁=0.95p₀，ω₂=10.01p₀

由此可见，低的主频率ω₁与车身固有圆频率p₀接近，高的主频率ω₂与车轮固有圆频率p_t接近，且有ω₁＜p₀＜p_t＜ω₂。

将两个主频率ω₁和ω₂分别代入式（2-60）和式（2-61），可确定两个主振型为一阶主振型：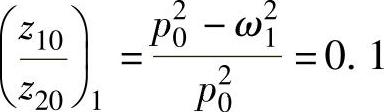

二阶主振型：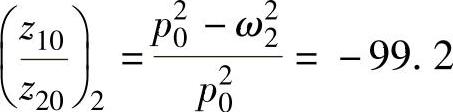

车身与车轮两个自由度系统的主振型如图2-12所示。在强迫振动情况下，激振频率ω接近系统主频率ω₁时将产生低频共振，按一阶主振型振动，车身质量m₂的振幅比车轮质量m₁的振幅大将近10倍，所以主要是车身质量m₂在振动，故称为车身型振动。

当激振频率ω接近系统主频率ω₂时，产生高频共振，按二阶主振型振动，此时车轮质量m₁的振幅比车身质量m₂的振幅大将近100倍（实际由于阻尼存在而不会相差这样多），故称为车轮振型振动。

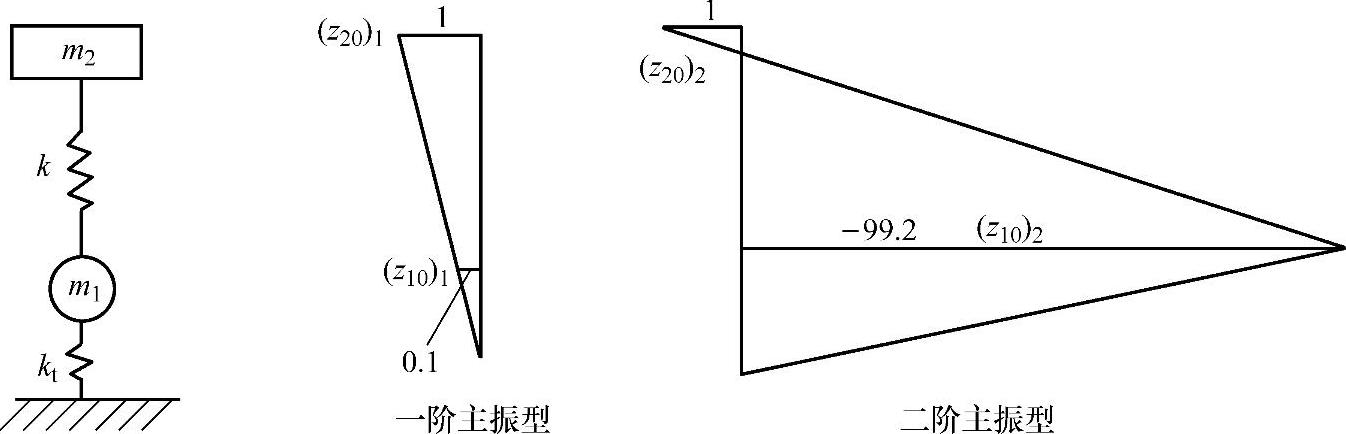
图2-12 二自由度系统的主振型

图2-12所示为二自由度系统的车轮振型振动，由于车身基本不动，所以可简化为图2-13所示的车轮部分的单质量系统，下面来分析车轮部分在高频共振区的振动。由图2-13可知，车轮质量m₁的运动方程为

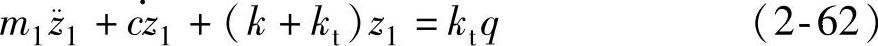
利用对单自由度系统的一般解法，可求得车轮位移z₁对路面激励q的频率响应函数为

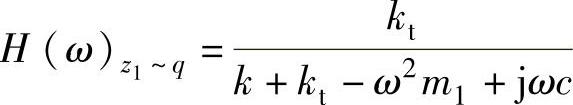
将上式分子、分母除以k+k_t，并把车轮部分固有频率p_t、车轮部分阻尼比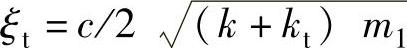以及λ_t=ω/p_t代入，可得

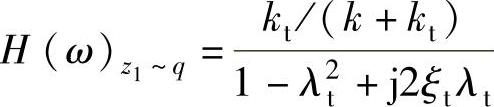
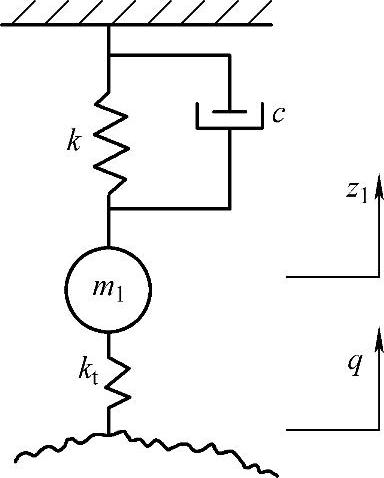
图2-13 车轮部分单质量系统

其幅频特性为

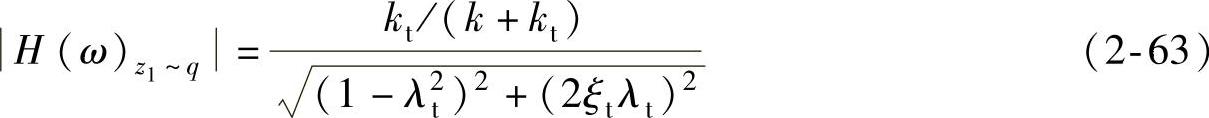
在高频共振ω=p_t时，车轮的加速度均方根值谱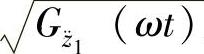正比于车轮响应加速度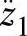对路面激励速度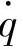的幅频特性，即

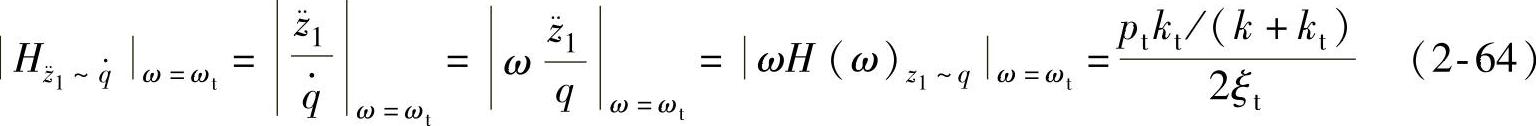
由式（2-64）可见，降低轮胎刚度k_t能使车轮固有圆频率p_t下降，使簧下质量系统的阻尼比ξ_t加大，这是减小车轮部分高频共振时加速度的有效方法。降低非悬架质量m₁，会使p_t和ξ_t都加大，车轮部分高频共振时的加速度基本不变，但车轮部分动载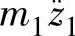下降，车轮相对动载F_d/G降低，有利于提高车辆行驶安全性。