汽车减振器仿真：单质量车身在路面激励下的振动响应

对式（2-8），通常关心其稳态随机响应，它取决于路面不平度函数随机激励q（x）和系统的频率响应特性函数H（ω）。由上可知，系统频率响应函数H（ω）z_-q为系统的振动响应z的傅里叶变换与激励q的傅里叶变换之比，即

式中，Z（ω）为响应z（t）的傅里叶变换；Q（ω）为激励q（t）的傅里叶变换。

对式（2-8）进行傅里叶变换，可得单质量车身在路面激励下响应的频响函数为

式中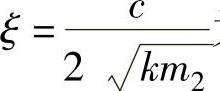，为阻尼比；λ为频率比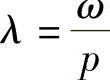，；ω为路面激励的圆频率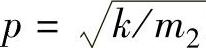；为系统固有圆频率。

由式（2-43）得为单质量车身在路面激励下的幅频特性和相频特性。

幅频特性为

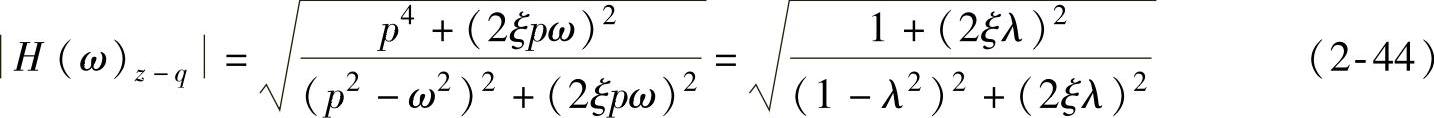
相频特性为

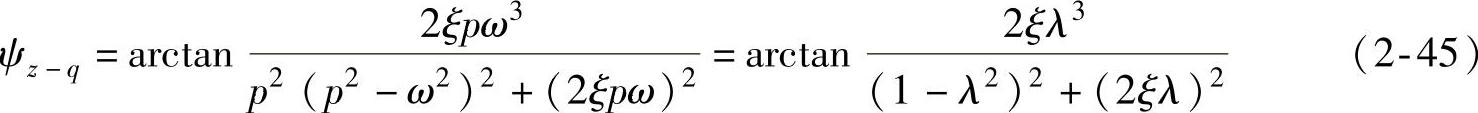
汽车在具有一定幅值的正弦波路面上行驶，即路面激励为

q（t）=asin ωt

则单质量车身在路面激励下的响应为

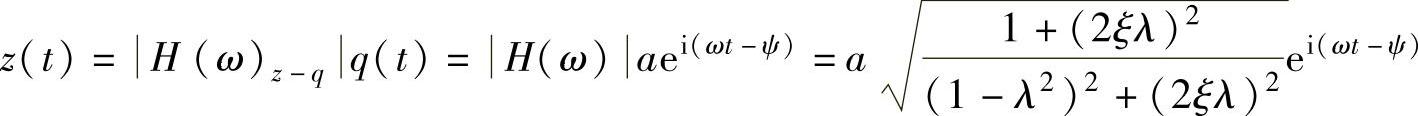
路面激励q（t）=asin ωt为正弦，所以系统的实际响应为

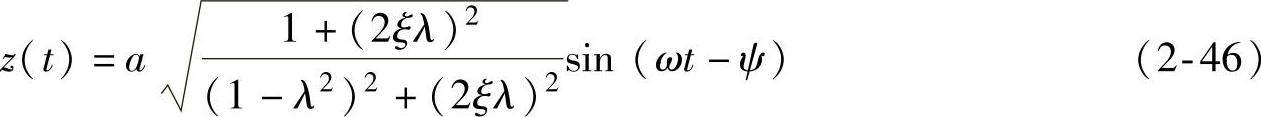(https://www.xing528.com)

式中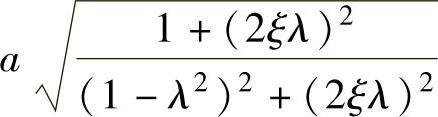，为幅值Z，即路面激励响应的幅值为

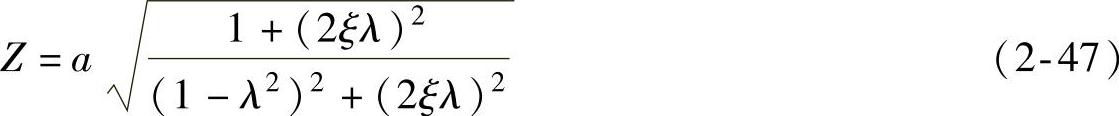
如果路面激励以速度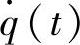=bsin ωt来表达，用上面同样的推导方法可得

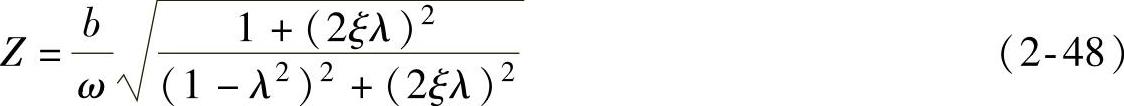
若以加速度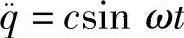来表达，则有

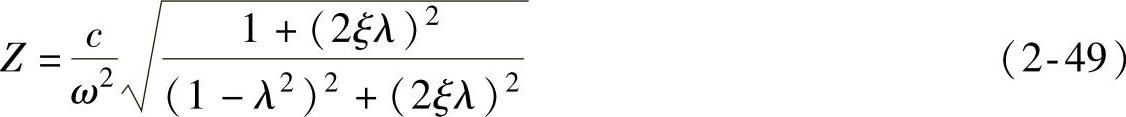
由H（ω）z_-q可以得到单质量系统的幅频特性曲线，如图2-10所示。

由频响函数式（2-44）和图2-10可知

1）当频率比λ=1时，系统出现共振，幅频特性达到最大，即共振时的幅值

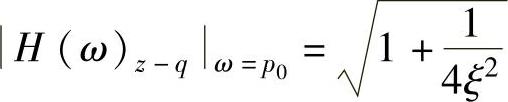
2）在低频段（0≤λ≤0.75），H（ω）z_-q略大于1，不呈现明显的动态特性，阻尼比对低频段的影响不大。

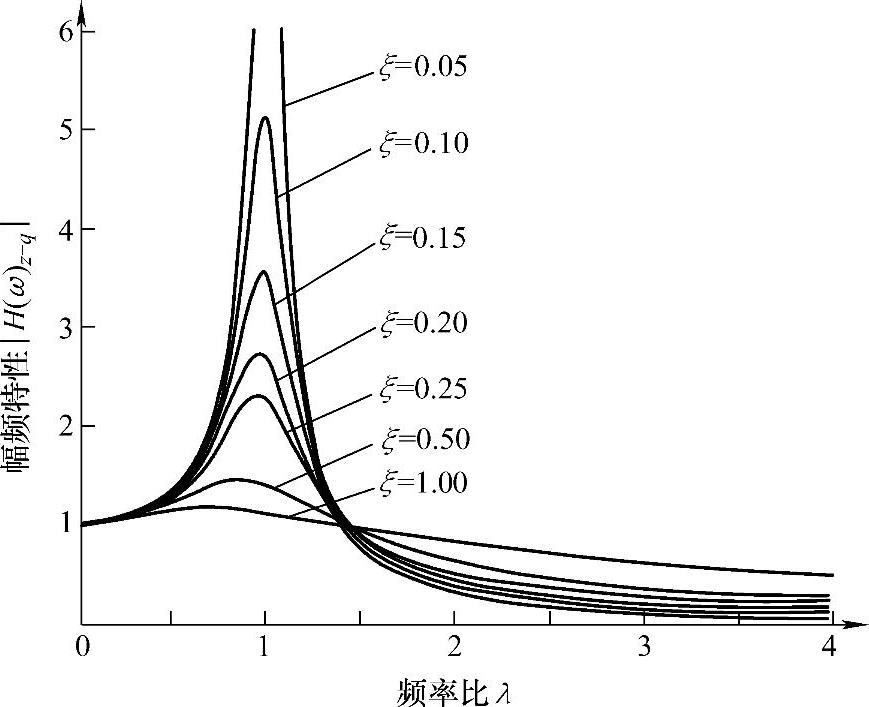
图2-10 单质量系统的幅频特性曲线

3）在共振段（0.75＜λ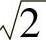＜），H（ω）z_-q出现峰值，将输入激励放大，增大阻尼比ξ，可使共振峰值明显降低。

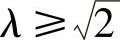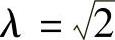4）在高频段（），当时，

H（ω）z_-q=1，系统响应与阻尼比ξ无关；当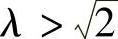时，H（ω）z_-q＜1，对输入位移有衰减作用，且阻尼比减小对减振有利。