【摘要】：单位谐波函数激励为复数形式的单位幅值简谐激振力，即fc=eiωt=cosωt+isinωt，则单质量系统的振动微分方程为单质量系统在单位谐波函数激励下的复数形式的响应为zc。它是一个由系统特性参数所确定的，表示系统在单位幅值的简谐激振力fc=eiωt作用下所产生的振幅。频率响应函数的模为，称为幅频特性。
单位谐波函数激励为复数形式的单位幅值简谐激振力，即fc（t）=eiωt=cosωt+isinωt，则单质量系统的振动微分方程为
单质量系统在单位谐波函数激励下的复数形式的响应为zc（t）。由于复数激振力和复数响应既是t的函数，又是ω的函数，故可令复数响应与复数激振力之比为H（ω），即
H（ω）被称为频率响应函数。它是一个由系统特性参数所确定的，表示系统在单位幅值的简谐激振力fc（t）=eiωt作用下所产生的振幅。对于简谐激励，若知道系统的频率响应函数，便可由式（2-32）可求得振动系统的输出响应，即
zc（t）=H（ω）fc（t）（2-33）
根据式（2-31），可得单位简谐激振力作用下的响应为
将上述三式代入式（2-32），两边消去eiωt，即得频率响应函数为
式中，λ为频率比，ξ为阻尼比。(www.xing528.com)
频率响应函数的模为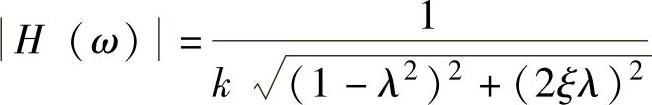
，称为幅频特性。
频率响应函数的相位差角为
，称为相频特性。
将复数形式的简谐激振力F0eiωt代入式（2-33），则复数形式的响应为
zc=H（ω）e-iψF0eiωt=F0H（ω）ei（ωt-ψ） （2-35）
若实际激振力为正弦函数F0sin ωt，则实际响应取复数形式响应的虚部，得实际解为
若实际激励为余弦函数F0cos ωt，则取复数形式响应的实部，得实际解为
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
