汽车减振器设计与自由振动仿真

令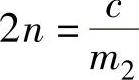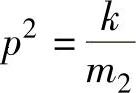，，当激励q=0时，则由式（2-8）可得单质量系统的自由振动微分方程为

式中，p为系统的固有圆频率；而阻尼对系统的影响，取决于n与p的比值ξ，称ξ为阻尼比，即

汽车悬架系统阻尼比ξ通常在0.25左右，属于小阻尼。因此，振动系统的齐次微分方程的解，也就是车身自由衰减的振动响应为

式中，A是由初始条件所决定的常数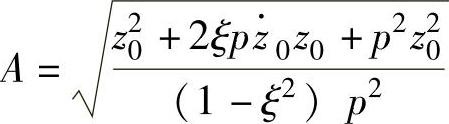，；φ是由初始条件决定的初相角，。

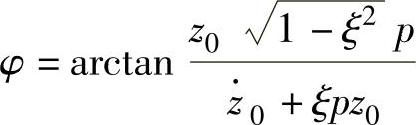由式（2-11）可知，有阻尼的自由衰减振动，车身质量m₂以有阻尼的固有频率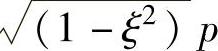振动，而振幅却按Ae^-ξpt规律衰减，如图2-7所示。

由上述可知，阻尼对自由振动有如下两方面的影响。

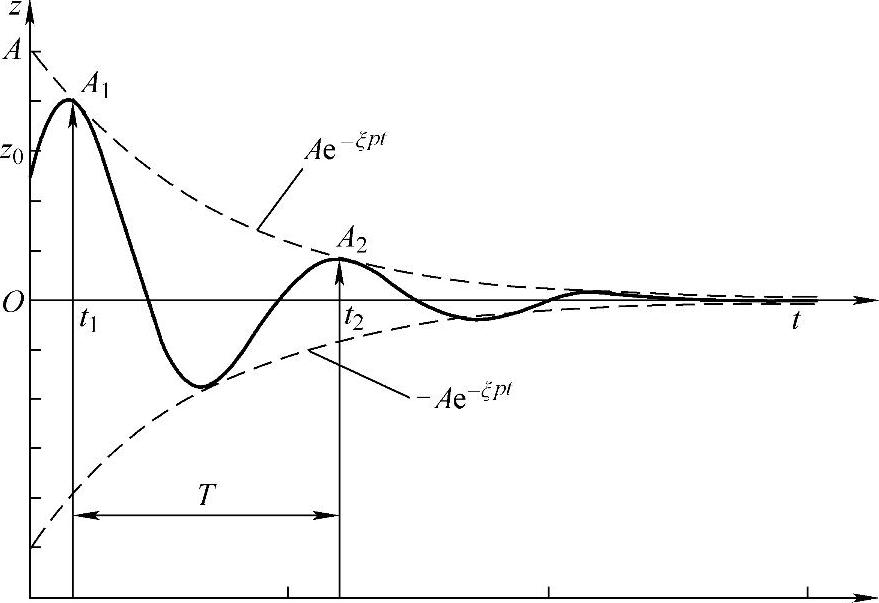
图2-7 自由衰减振动曲线

1.阻尼使固有频率降低

如果无阻尼自由振动系统原固有频率为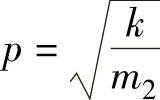，则弱阻尼悬架系统的固有频率p′为

(https://www.xing528.com)

因此，可知小阻尼悬架系统的固有频率p′随阻尼比ξ的增大而降低。

由于汽车悬架系统的阻尼比ξ约为0.25，因此，阻尼是悬架系统的固有频率仅下降了3%左右，可以忽略不计，所以，工程上小阻尼振动系统的固有圆频率p′，可以近似地认为等于无阻尼振动系统的固有圆频率p，即p′≈p。因此，车身振动的固有圆频率和固有频率，分别为

2.阻尼决定振幅的衰减程度

设相邻两振幅分别为A_i和A_i+1（图2-7），它们的比值η称为减幅系数

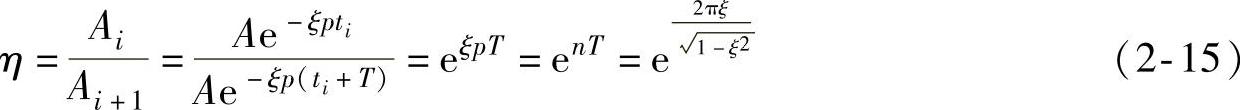
式中，n为衰减系数。n越大表示阻尼越大，振幅衰减也就越大。令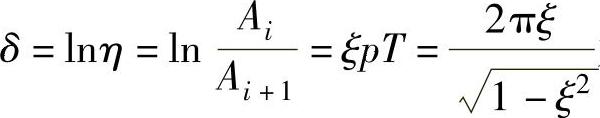为对数衰减率，因此可得

所以，由式（2-16）可得振动系统的阻尼比为

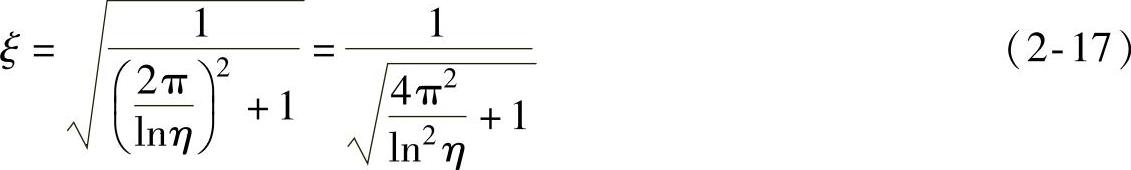
若ξ≪1，则由式（2-16）得，lnη≈2πξ，因此由式（2-17）可知，小阻尼车辆悬架系统的阻尼比可近似表示为