振动学知识：汽车振动频率与载荷无关

如图4－7所示，在振动学中，最简单的振动模型由一个质量块和一根弹簧组成。

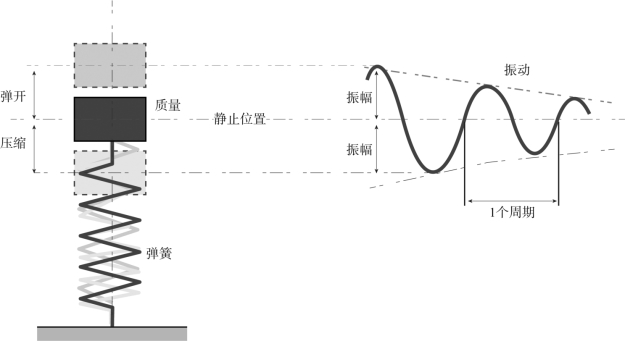
图4－7　最简单的振动模型

式中，k——弹簧刚度（德文为Koeffizient，英文为Coefficient）；

m——质量（Mass）；

f——频率（Frequency）。

公式（1）说明振动周期或频率是不会因外界冲击力的大小发生变化的，这个原理相当于挂钟钟摆的摆动周期为1s，将摆动量（幅值）人为增加，但周期仍是1s 的道理一样。这说明模型的振动频率是不变的，这个不变的频率称为固有振动频率。人最适应的心脏的跳动频率在1.0～1.5 Hz，汽车悬架一般按1.1 Hz 的固有振动频率调校，调校时k和m 的比值不能变化，才能保证是1.1 Hz，那么就要求刚度k 的变化率和质量m 的变化率要相同。(www.xing528.com)

若将这个理想的振动模型放在空气中，振动会持续较长时间，若将这个理想的振动模型放在水中，振动会持续较短的时间，幅值为0 后停止，这说明水的阻尼比空气的大。如图4－8所示，汽车上的减震器相对于汽车，就相当于水相对于重块一样。汽车的振动学由这样的简单模型经过组合而成，实际开发要经过振动仿真和真实振动实验来确认系统的固有振动频率，仿真时的基础就是这个最基本的模型。

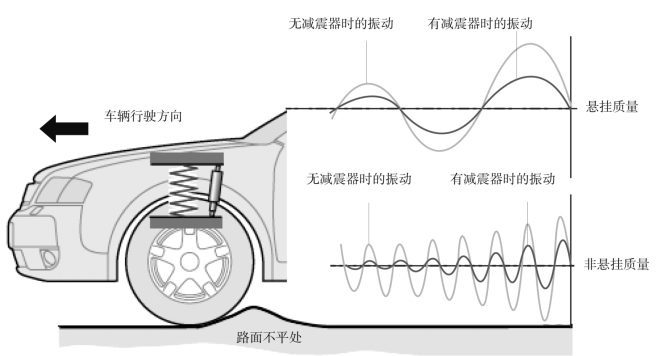
图4－8　有无减震器的系统对比

如图4－9所示，增加车内重物的质量和用软一点的弹簧，系统的固有振动频率减小；而减小车内重物的质量和用硬一点的弹簧，系统的固有振动频率增大。

图4－9　不同载荷对车身振动的影响

幅值和外激的强度有关，但不会改变系统的振动频率。频率与系统的k 和m 的参数有关，一般高挡轿车把前桥悬架频率比后桥调得低一些，比如前桥为1.13 Hz，而后桥为1.33 Hz。