建筑设备工程2版：定态流体系统质量守恒

如图1-5所示的定态流体系统，流体连续地从1—1截面进入，从2—2截面流出，且充满全部管道。以1—1、2—2截面以及管内壁为衡算范围，在管路中流体没有增加和漏失的情况下，单位时间进入截面1—1的流体质量与单位时间流出截面2—2的流体质量必然相等，即

或

推广至任意截面，有

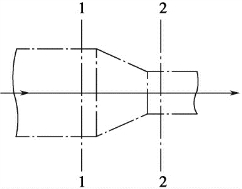
图1-5　连续性方程的推导

式（1-6）～式（1-8）称为连续性方程，表明在定态流动系统中，流体流经各截面时的质量流量恒定。

对不可压缩流体，ρ=常数，连续性方程可写为

对于圆形管道，式（1-9）可变形为(www.xing528.com)

【例1-1】　如图1-6所示，管路由一段φ89mm×4mm的管1、一段φ108mm×4mm的管2和两段φ57mm×3.5mm的分支管3a及3b连接而成。若水以9×10-3m3／s的体积流量流动，且在两段分支管内的流量相等，试求水在各段管内的速度。

【解】　管1的内径为d1=89-2×4=81mm，则水在管1中的流速为

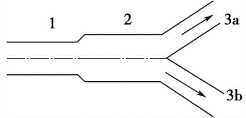
图1-6　管路图

u1=1.75m／s

管2的内径为d2=108-2×4=100mm。由式（1-10），则水在管2中的流速为

u2=1.15m／s

管3a及3b的内径为d3=57-2×3.5=50mm。因水在分支管路3a、3b中的流量相等，则有

u2A2=2 u3A3

即水在管3a和3b中的流速为

u3=2.30m／s