城市风道量化模拟分析与规划设计

1.置入几何模型

通常来讲，导入到CFD软件中的几何模型可以分为二维模型和三维模型两种。对二维模型进行分析可以得到二维平面上的流场信息，但是无法得到第三空间维度上的信息。如果要量化分析城市风场在三维空间的分布特征，则需要导入三维空间模型来开展分析。本书主要揭示不同类型风道在不同风道宽度和建筑高度条件下的城市风道通风效果，因此，需要获取3个空间维度上的风场信息。CFD软件为Fluent，目前集成在Workbench工作平台中，该平台包括一系列前处理软件，包括建模和划分网格，被广泛使用的主要有Gambit、Mesh、ICEM CFD等。本书利用Mesh划分网格，分为三组进行对照组模拟分析。具体是将建立好的城市风道三维模型置入Mesh软件中，并且设置好模拟的初始条件。导入Mesh中的文件为sat格式。另外，为了方便在后处理软件CFD-POST中进行切面生成操作，需尽量将模型中的一个角点建立在坐标原点，同时尽量将风道方向调整为正南北或正东西走向。将模型置入Mesh软件后，即可为划分网格做准备（见图4-2）。

图4-2　置入ANSYS Mesh中的三维模型

2.划分网格

在实际的模拟仿真工作中，大约有80%的时间用于划分网格，可以说网格生成的效率直接影响到模拟工作的效率。目前被广泛使用的划分网格的软件主要有Gambit、Mesh、ICEM CFD等，各自具有其优缺点和适用性。

Gambit是Fluent公司根据CFD计算的特殊要求而开发的前处理软件，使用映射网格划分技术，能自动对几何对象进行分割，适合逻辑形状为三角形或四边形的面，在几何形状不复杂时，能生成高质量网格，但是版本无更新。Mesh网格划分平台具有参数化、稳定性、高度自动化、灵活性、物理相关以及自适应结构等特点，尤其适合复杂模型网格的划分，对于简单模型优势则不够突出。ICEM CFD网格划分功能强大，不仅能划分非结构化网格，还能划分结构化网格，这也是其备受用户青睐的原因，对于复杂模型可以手动设置网格节点分布，但工作量较大，其建模功能也较弱。各软件划分网格的优缺点以及适用性与算法有关^[1]（见表4-1）。

表4-1　几种典型网格生成算法对比

本章选用的网格划分软件为Mesh，需将对照组的9个模型都划分网格，网格为非结构化四面体网格。非结构化网格的优势在于，它不受解域的拓扑结构与边界形状限制，能够根据流场特征自动调整网格密度，适合街区尺度的城市风环境模拟研究，也能够保证计算结果更接近实际^[2]。

首先在ANSYS Workbench中打开Mesh，然后通过Geometry导入建立的sat文件，选择几何表面进行命名，分别表示进口（inlet）、出口（outlet）、建筑群空隙表面（a）、风道表面（b）、其余表面默认为壁面（wall）。采用高级网格划分功能为曲面，关联中心缺省值为粗糙（coarse），平滑度为中等（medium），选择过渡模式为慢（slow），网格最小尺寸为默认的0.28633mm，网格最大尺寸为4mm，最小边缘长度0.5mm，膨胀率为默认值1.2（见图4-3）。需要说明的是，原模型尺寸大小为400m×400m，若按照该尺寸划分网格，生成的网格数量巨大，导致后期解算过程异常缓慢。根据流体力学相似性定理，可以采用缩尺模型进行计算，即将原尺寸缩小一定比例后，再进行划分网格及求解运算。将所有模型按照等比例缩小1000倍后进行网格划分。生成结果显示，网格数量仍达到百万级别，经检查网格质量后未出现负向体积，网格质量良好。

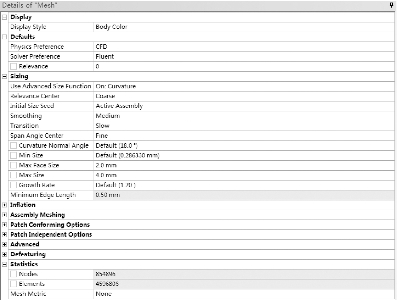
图4-3　网格划分参数设置

设置好参数之后，执行生成网格操作。以d30h48r00模型（表示风道宽度为30m，建筑高度为48m，风道粗糙度为0m，水体型风道）为例，生成网格4608755个，面9391707个，节点857150个（见图4-4、图4-5）。对网格体积进行检查，发现未出现负向体积，minimum orthogonal quality以及maximum aspect ratio指标均满足要求。

图4-4　风道模型的计算空间网格

图4-5　风道模型壁面wall网格

在划分网格过程中，将网格由疏到密逐渐加密进行网格敏感性测试。多次测试表明，由于研究区域模型较大，网格生成效率以及计算效率很低。根据流体力学相似性原理对模型缩小1000倍后，网格生成效率以及计算效率显著提高，且对网格敏感性存在一定影响。对缩放后模型进行网格敏感性测试，最终确定当最大网格尺寸为4mm、最小网格尺寸为0.3mm左右时，网格依赖度处于较低水平。

3.设置边界条件

选取k-ε湍流模型，定义边界条件。

（1）入流边界

流场入口采用速度进口（velocity inlet），受城市下垫面粗糙度的影响，风在穿过街区的过程中能量发生衰减，风速降低，而其本身结构也会发生变化。一般情况下，地面以上300m（小于1000m）范围内均属于大气边界层范围，这个范围以上的风速不会受到地表粗糙度的影响，可以在大气梯度作用下自由流动^[3]。近地面入口的风速服从指数方程分布

式中：u为距地面z高度处的风速，单位为m/s；u0为参考高度处的风速；z0为气象站风速测点高度，一般为10m；α为地面粗糙度。

对照组建立的三维空间模型中的风道方向均为南北向，街区为规则的400m×400m方形地块，以垂直于风道方向的上边线作为速度入口，10m高度处初始速度为3m/s。

（2）出流边界

定义流场出口为压力出口（outflow），以垂直于风道方向的下边线作为压力出口，假设出流面上的流动已经充分发展，流动已经恢复为无阻碍的正常流动，出口压力为零。

（3）天空高度

考虑到模型中建筑高度最高仅为72m，将模型的天空高度设为100m，既可保证模拟所需的正常环境，也可减少网格数量，提高运算效率。

（4）其他边界

计算边界的划定与计算域有关。在选取计算域时未在研究区域四周延伸一定区域，主要有两个原因：首先，需对街区通风的风速比例进行定量化研究，这决定了研究区域需为封闭空间。多数CFD指南中在选取计算域时，通常在研究区域四周进行一定的延伸，这主要适用于无须求解研究区域风速比例的情况。若对研究区域四周进行延伸，在对研究区域设置边界条件时会遇到困难。因此本书未采取相关指南中对研究区域进行延伸的做法。其次，在研究范围四周进行延伸后增加了模型计算量，降低了数值运算效率。将街区的范围线作为侧面边界，即围合的400m×400m边界，建筑物表面和建筑物固定不动，采用无滑移壁面（no slip wall）条件。

4.求解设置

设定重力参数gravity的值为-9.8m/s2。流体材料设置为空气。选取湍流模型为标准k-ε模型，适用于初始迭代、设计选型以及参数研究，其余参数默认，即Cμ=0.09，Cε1=1.44，Cε2=1.92，σk=1，σ∈=1.3。本章采用SIMPLEC算法，收敛准则为连续性绝对残差、动量项绝对残差以及湍流动能绝对残差小于0.001。与软件默认的SIMPLE算法相比，SIMPLEC算法改进了速度修正公式，解决了速度修正不协调问题，其压力不再需要松弛，收敛性速度更快。

5.风道风场影响因素甄别与分析

模拟分3组进行，涉及9个模型，共模拟27次。现分别对每组情况进行说明。以下对相关图表的命名规则为“d+宽度+h+高度+r+粗糙度+vc（或vv，或pc，或vh）”，其中vc表示速度分布云图，pc表示风压分布云图，vv表示速度矢量云图，vh表示速度分布直方图。例如宽度为30m，高度为48m的水体型风道的速度分布云图名称为“d30h48r00vc”。

城市风道通风环境质量的评价标准为，小于1.5m/s速度比例越低越好，1.5～5m/s速度比例越高越好，大于5m/s速度比例越低越好，当最大风速大于5m/s时，最大风速越小越好。

在对城市风道宽度、建筑高度、城市风道类型进行研究时，将城市风道宽度取值为30m、40m、50m、80m、100m，将建筑高度取值为24m、36m、48m、60m、72m，在对结果进行分析时，根据风速比例随变量取值的变化情况来判断最优取值区间以及最优值，即最优取值区间的节点受到变量取值的精细程度的影响。本章将风速比例及最大风速作为城市风道通风能力的评价标准，认为其差异大到足以判断取值区间。若考虑计算次数过少带来的误差，可能存在一个误差范围，后续研究中可进一步深化。

（1）第一组，以风道宽度为变量

这一组需要用到5个模型，共模拟15次，以宽度为变量，风道宽度分别为30m、40m、50m、80m、100m，建筑高度为48m，道路型风道、绿地型风道、水体型风道的粗糙度分别为0.0013m、0.0052m、0m。运用CFD-POST后处理软件，从每次运算结果中获取风速分布云图、风速矢量云图、风压分布云图和风速分布直方图。首先是对风速分布云图的分析。在CFD-POST中，可以选择查看全局范围内的风速分布云图，也可以查看x、y、z这3个方向中任意方向截取的局部云图，还可以查看风速分布直方图。因为主要是要通过考察距离地面行人高度1.5m处的风速比例来评价城市通风环境，所以本书截取z轴方向高度为1.5m的切面作为分析面。下文中，风速分布云图及风速矢量云图均是取自距离地面行人高度1.5m处。风压属于人体较难感知的气象学参数，当风速较低时，风压对人体造成的不适感并不强烈，因此不对其进行详细分析。由第一组模拟结果可选择生成15幅速度分布云图、15幅速度矢量云图、15幅速度分布直方图。

1）道路型风道（粗糙度设定为0.0013m，图表中缩写格式为r0013）

由道路型风道的风速云图（图4-6、图4-7）可知，在初始速度为3m/s的风速下，风速在部分区域会超过初始速度，根据流体的质量守恒方程，这种情况为正常现象。当风道宽度为30m时，建筑侧向区域风速的连续性好于中间的风道，但是风道边缘受到扰动较小，直观上表现为风速矢量箭头趋向性更好，湍流现象不严重。随着风道宽度的增大，风道中的风速连续性明显好于其他区域，且湍流现象进一步减弱，而其他区域变化情况与之相反，但这时街区内静风区域面积仍然较大，是城市通风环境质量较差的表现。当风道宽度为50m时，静风区面积明显减小，表明通风状况良好。当风道宽度增大到80m时，风道内风速大于1.5m/s的区域较多，静风区面积进一步减小；当风道宽度进一步增大到100m时，风速开始降低，静风区域增多。

图4-6　第一组道路型风道速度分布云图

图4-7　第一组道路型风道速度矢量云图

由风速分布直方图（图4-8）可知，当风道宽度为30m时，整个街区内的最大风速为3.72m/s，风速区间为1.5～3.72m/s的比例为63%，1.5m/s以下风速比例为37%。当风道宽度为40m时，整个街区内的最大风速为3.73m/s，风速区间为1.5～3.73m/s的比例为63%，1.5m/s以下风速比例为37%。当风道宽度为50m时，整个街区内的最大风速为3.67m/s，风速区间为1.5～3.67m/s的比例为67%，1.5m/s以下风速比例为33%。当风道宽度为80m时，整个街区内的最大风速为3.68m/s，风速区间为1.5～3.68m/s的比例为67%，1.5m/s以下风速比例为33%左右；当风道宽度为100m时，整个街区内的最大风速为3.79m/s，风速区间为1.5～3.79m/s的比例为65%，1.5m/s以下风速比例为35%（见表4-2）。

图4-8　第一组道路型风道速度分布直方图

表4-2　第一组道路型风道风速指标

随着风道宽度的增大，风速大于等于1.5m/s比例保持动态稳定，最大风速虽有波动但仍可视为呈增大趋势。可初步判断，在所选宽度中，当风道宽度在50～80m时，道路型风道的通风效果较好，结合风速云图可进一步判断出80m宽度时通风效果最佳。

2）绿地型风道（粗糙度设定为0.0052m，图表中缩写格式为r0052）

由对绿地型风道的风速云图（图4-9、图4-10）分析可知，当风道宽度为30m时，风道边缘受到扰动较小，但是存在较多静风区域。当风道宽度为40m时，静风区域面积明显增大，不利于形成良好的城市风环境。当风道宽度为50m时，风道中的风速连续性明显好于其他区域，静风区域面积逐渐减小。当风道宽度增大到80m时，静风区域面积达到最小，风道的通风环境达到最佳。当风道宽度进一步增大到100m时，风道内大部分区域风速已经降低至1.5m/s以下。总体来说，绿地型风道宽度增大过程中，其通风环境变化规律与道路型风道相似。

图4-9　第一组绿地型风道速度分布云图

风速分布直方图分析的结果可整理为表4-3。

图4-10　第一组绿地型风道速度矢量云图

表4-3　第一组绿地型风道风速指标

由对风速分布直方图（图4-11）的分析可知，随着风道宽度的增大，最大风速逐渐增大并在50m宽度左右开始降低，而大于等于1.5m/s的风速比例基本呈增加趋势。这表明对于绿地型风道而言，宽度在50～80m时通风效果较好。单就直方图数据来看，难以确定宽度最优值，但结合风速云图来进行分析，可初步判断在所选宽度中80m宽的绿地型风道对于整个街区的通风效果达到最佳。

3）水体型风道（其粗糙度设定为0m，图表中缩写格式为r00）

图4-11　第一组绿地型风道速度分布直方图

图4-12　第一组水体型风道速度分布云图

由水体型风道的风速云图（图4-12、图4-13）可知：当风道宽度为30m时，风道边缘受到扰动较小，同时静风区域较大；当风道宽度为40m时，风道边缘受到扰动增大，湍流逐渐增强，静风区域面积开始减小；当风道宽度为50m时，随着宽度的增加，峡谷效应减弱，风道边缘受到扰动变小，静风区域面积进一步减小。当风道宽度增大到80m时，风速大于等于1.5m/s的区域增多，静风区域面积明显减小，风道的通风环境达到最佳。当风道宽度进一步增大到100m时，风道内大部分区域风速已经降低至1.5m/s以下。而除风道以外的其他区域难以形成连续的风场，风路径容易被围合式建筑排布方式引起的湍流稀释，从而影响整体通风效果。

图4-13　第一组水体型风道速度矢量云图(www.xing528.com)

风速分布直方图分析的结果可整理为表4-4和图4-14。

表4-4　第一组水体型风道风速指标

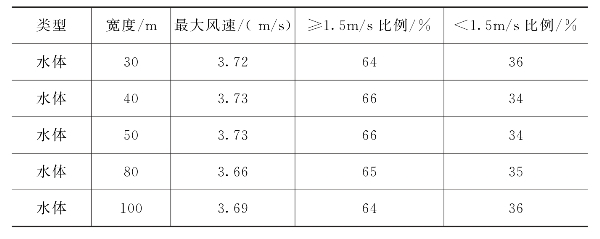
单就风速分布直方图数据可知，随着风道宽度的增大，水体型风道最大风速和大于等于1.5m/s风速比例总体上在40～80m维持较高水平，结合风速云图可进一步判断80m宽度为最佳值。因此，对于道路型风道和绿地型风道而言，其适宜的宽度为50～80m，以80m为最佳；对于水体型风道而言，其适宜的宽度为40～80m，最佳值为80m。取公共部分后得到这三种风道的适宜宽度为50～80m，以80m为最佳。

图4-14　第一组水体型风道速度分布直方图

综上所述，不管是哪种风道，都表现出共同的特征，即风道宽度越大，通风效果越好。风道的适宜宽度为50～80m，80m宽度时的风道通风效果最好。在该取值区间状态下，从云图上来看，基本呈现风速连续性强，静风区小等特点，比较利于形成良好的城市通风环境；从指标来看，小于1.5m/s风速比例较低，1.5～5m/s风速比例较高，大于5m/s风速比例较低；最大风速均小于5m/s。

（2）第二组，以建筑高度为变量

这一组模型需涉及9个模型，模拟12次（原本需模拟15次，但在第一组模拟已经完成的情况下，除去第一组中已经模拟的3次，只需再模拟12次），其中有5个模型在第一组中已经构建，仅需新增4个模型，建筑高度分别为24m、36m、60m和72m，风道宽度为50m。为控制变量，本组模拟中不考虑建筑日照间距随建筑高度的变化。本章所讨论的对照组模型中的建筑前后间距均为48m。

1）道路型风道

图4-15　第二组道路型风道速度分布云图

图4-16　第二组道路型风道速度矢量云图

由风速分布云图和风速矢量云图（图4-15、图4-16）可知，在风道宽度均为50m的条件下，随着建筑高度的增大，峡谷效应逐渐明显，表现为风道及建筑侧向距离空气流场的边缘弱风区厚度逐渐增加，入口处高风速区域衰减较为明显，静风区域面积总体保持减小趋势。当建筑高度为48m时，静风区域面积达到最小，随着高度的持续增加，静风区域面积又逐渐增大。因此，可初步判断当建筑高度为48m时道路型风道能达到最佳通风效果。为了佐证该判断，还需进一步对风速分布直方图进行分析。

由道路型风道的风速分布直方图（图4-17）和表4-5可知，随着建筑高度的增大，街区内的最大风速呈逐渐增大趋势，而大于等于1.5m/s风速比例呈逐渐降低趋势，风速小于1.5m/s的弱风比例则逐渐增大，表明静风区域面积也逐渐增大，不利于良好城市风环境的形成。由此可知，对于改善街区通风环境而言，合适的建筑高度应在24～48m，而高度为48m时，街区内静风区域面积最小，整体通风环境达到最佳。

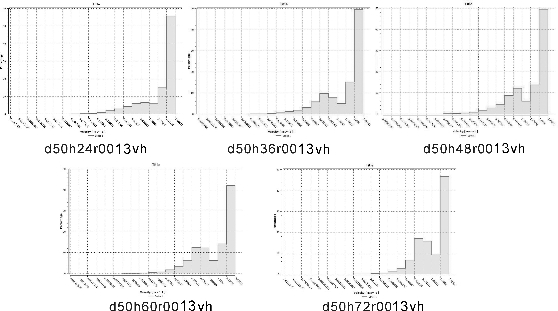
图4-17　第二组道路型风道速度分布直方图

表4-5　第二组道路型风道风速比例

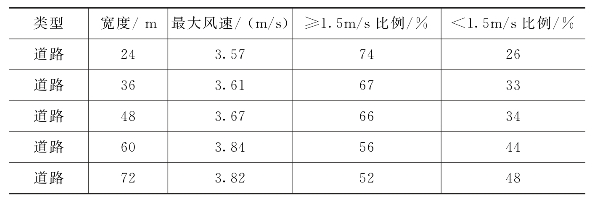
考虑到模型中24m、36m高度的建筑前后间距均大于实际情况，而60m、72m高度的建筑模型的前后间距又小于实际情况，再考虑到用地的经济性，宜将48m作为合适的建筑高度。通过结合速度云图、速度直方图结果以及用地的经济性，最终确定适宜建筑高度为24m～48m，以48m为最佳。

2）绿地型风道

图4-18　第二组绿地型风道速度分布云图

图4-19　第二组绿地型风道速度矢量云图

其风速分布云图以及风速矢量云图（图4-18、图4-19）表明，随着建筑高度的增大，风道峡谷效应依然呈增大趋势，风道边缘弱风区厚度持续增加，静风区域面积在动态中呈减小趋势，在高度为48m时达到最小，随后又逐渐增大。湍流呈周期性规律，可能导致风速峰值不断上升。

将对风速分布直方图（图4-20）的分析结果整理成表4-6。

图4-20　第二组绿地型风道速度分布直方图

表4-6　第二组绿地型风道风速指标

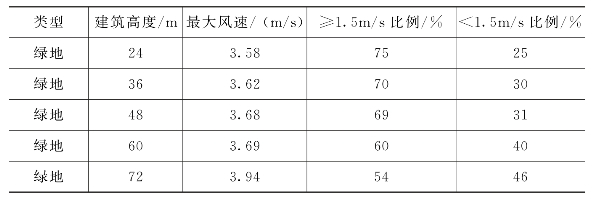
综合对绿地型风道的风速分布云图以及风速分布直方图的分析可知，随着建筑高度的增大，街区内的最大风速也呈逐渐增大趋势，同样是受到峡谷效应影响，而风速大于等于1.5m/s的比例呈逐渐降低趋势，风速小于1.5m/s的弱风比例则逐渐增大，不利于良好城市风环境的形成。因此，对于绿地型风道而言，在促进街区尺度通风方面，合适的建筑高度应为24～48m，尤以48m为最佳。

3）水体型风道

图4-21　第二组水体型风道速度分布云图

图4-22　第二组水体型风道速度矢量云图

其风速分布云图和风速矢量云图（图4-21、图4-22）显示，随着建筑高度的增大，风道峡谷效应依然呈增大趋势，风道边缘弱风区厚度持续增加，静风区域面积也在逐渐增大，湍流呈周期性出现规律，可能导致风速峰值不断上升。其变化规律与道路型风道和绿地型风道相似，在建筑高度为60m时湍流强度达到较高水平，随后开始减弱。风场的湍流强度与流通区域空间形态和风速有关，围合式或半围合式建筑排布容易导致湍流形成。湍流强度过大会导致局部风流速加快，风速大于5m/s会对人体产生危害，因此应尽量减弱湍流强度。建筑高度在36m以下时，静风区域面积基本保持在较低水平，在48m高度处出现明显增大，随之又开始减小。水体型风道静风区域面积变化规律与前两种存在偏差，其原因可能是风道粗糙度骤降为0m导致，说明粗糙度对城市通风效果的影响较大。

由水体型风道的风速分布直方图和风速指标（图4-23、表4-7）可知，当建筑高度为72m时，街区风场中最大可产生3.82m/s的风速，但其风速在1.5m/s以下比例达到51%，弱风面积太大不利于街区空气流通和污染物扩散，影响通风环境和空气质量；当建筑高度在24～48m时，最大风速为3.56m/s，1.5～3.56m/s区间风速比例为76%，弱风比例为24%，风环境良好；随着建筑高度的增加，最大风速和弱风比例也呈增大趋势，风速增加幅度小于弱风比例增加幅度。在城市风环境评价中，当风速达到标准时，更多需考虑减小弱风比例，以增强城市通风。因此，对于水体型风道而言，在选取研究的建筑高度数值中，建筑高度宜在24～48m，以48m为最佳。

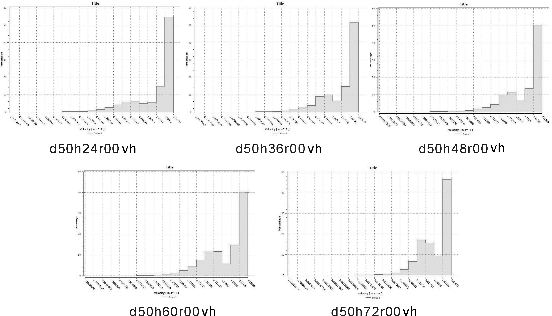
图4-23　第二组水体型风道速度分布直方图

表4-7　第二组水体型风道风速指标

（3）第三组，以风道类型为变量

第三组研究城市风道类型对于街区通风效果的影响，其关键在于通过设置模型的粗糙度来对城市风道类型加以区分。根据上文研究结果可知，道路型风道、绿地型风道和水体型风道表面的粗糙度分别为0.0013m、0.0052m、0m，建筑高度均为48m。为保证研究更加充分，分析不同风道宽度情况下的通风情况。本组模拟可以直接采用第一组模拟的结果，建筑高度设定为48m。当风道宽度分别为30m、40m、50m时，各类型城市风道风速云图及速度分布直方图的规律见图4-24到图4-32以及表4-8。

图4-24　第三组30m宽度风道速度分布云图

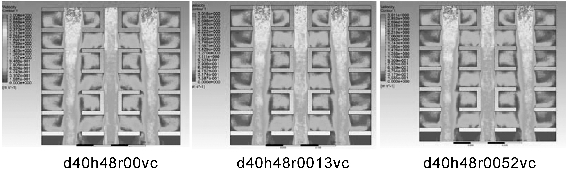
图4-25　第三组40m宽度风道速度分布云图

图4-26　第三组50m宽度风道速度分布云图

图4-27　第三组30m宽度风道速度矢量云图

图4-28　第三组40m宽度风道速度矢量云图

图4-29　第三组50m宽度风道速度矢量云图

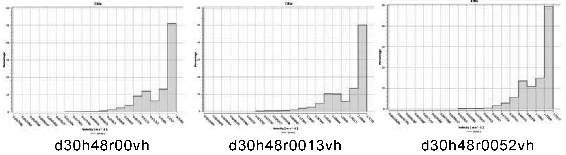
图4-30　第三组30m宽度风道速度分布直方图

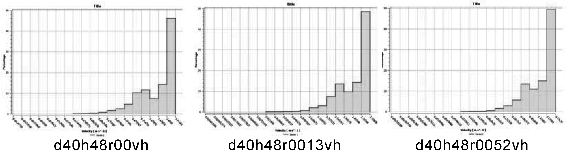
图4-31　第三组40m宽度风道速度分布直方图

图4-32　第三组50m宽度风道速度分布直方图

表4-8　第三组各类型风道风速比例

单从云图信息来看，该截面上静风区域面积随着风道表面粗糙度增大而减小，因此容易产生风道表面空气动力学粗糙度越大，静风区域面积越小的结论。另外，造成该现象的原因可能是风道表面粗糙度突变时形成高强度湍流，从而在部分区域内形成空气扰动，进而在一定程度上加快了风的流通。要论证该结论的正确性，需进一步通过直方图信息来进行验证。

不同类型城市风道的风速分布直方图数据显示，城市风道类型，即城市风道表面粗糙度对于整个街区内的最大风速影响较小，三种城市风道类型在大于等于1.5m/s的风速区间上的比例都在59%～64%。不同风道宽度的统计数据表明，在风速大于等于1.5m/s的速度比例指标上，水体型风道大于道路型风道，道路型风道大于绿地型风道，这表明水体型风道的通风能力优于道路型风道，道路型风道优于绿地型风道。可初步得出的结论为，三种城市风道类型中，水体型风道通风效果最佳。因此，在对照组实验状态下，即当距地面10m高度处初始风速为3m/s时，可以初步认为空气动力学粗糙度依次为0.0013m、0.0052m、0m的道路型风道、绿地型风道、水体型风道，其通风能力优越性为水体型风道最佳，道路型风道次之，绿地型风道最差。

综上所述，在道路型风道、绿地型风道和水体型风道中，若假设其表面粗糙度依次为0.0013m、0.0052m、0m，则通风能力最好的为水体型风道，其次为道路型风道，最后为绿地型风道；在选取的风道宽度依次为30m、40m、50m、80m和100m时，风道宽度宜在50～80m，以80m为最佳，超过此数值后，风道通风效果提升潜力降低；在选取的建筑高度依次为24m、36m、48m、60m和72m时，建筑高度以24～48m为宜，最适宜的建筑高度为48m，低于该值不利于用地经济性的提升，高于该值则不利于提升城市通风环境质量。通过对照组的模拟分析，研究了城市风道在不同的风道类型、风道宽度和建筑高度条件下的通风效果，并对每种风道类型进行了量化模拟。