深基坑围护设计解析-三种挡土结构解析方法

挡土结构的解析法主要有三种方法：山肩邦男法、弹性法和弹塑性法。前两种方法都假定土压力已知且横撑轴力及挡土结构弯矩在下道支撑设置以后均不变化，它考虑了挡土结构的变形，但未考虑支撑的变形。横撑轴力和挡土结构弯矩不变化可作如下理解：

（1）下道横撑设置以后，上道横撑的轴力不变。

（2）下道横撑支点以上的挡土结构变位是在下道横撑设置前产生的。

（3）下道横撑支点以上的挡土结构弯矩是在下道横撑设置以前产生的。

由此可知，该两种方法都假定挡土结构的内力及支撑轴力与开挖过程无关。弹塑性法假定土压力已知，但横撑轴力和挡土结构弯矩随开挖过程变化，它考虑挡土结构和支撑的变形。

精确解在绪论中已有介绍，为简化计算，山肩邦男提出了如下近似解法，其基本假定如下（图8-10）：

1.基本假定

（1）在黏土地层中，挡土结构作为底端自由的有限长弹性体。

（2）同精确解。

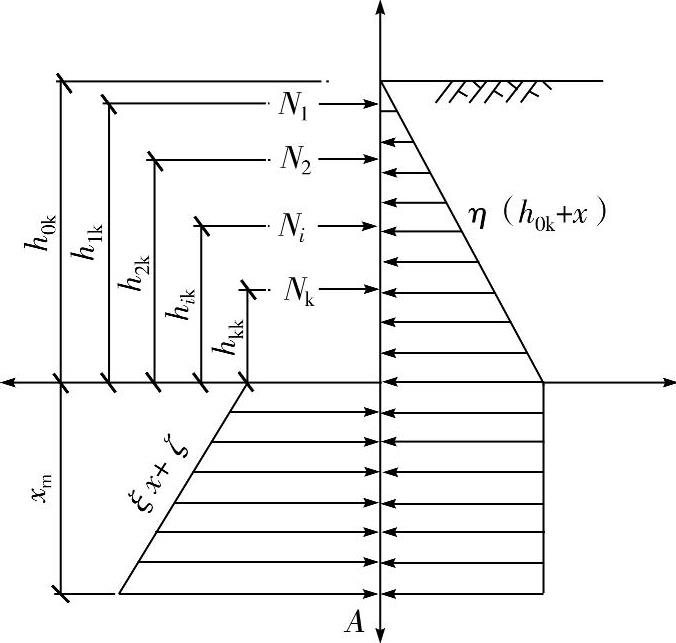
图8-10 山肩邦男法近似解计算简图

（3）开挖面以下土的横向抵抗反力取为被动土压力，其中（ξx+ζ）为被动土压力减去静止土压力（η_x）后的数值。

（4）、（5）同精确解。

（6）开挖面以下挡土结构弯矩M=0的点假想为一个铰，而且忽略此铰以下的挡土结构对此铰以上挡土结构的剪力传递。(www.xing528.com)

2.计算步骤

近似解法只需应用两个静力平衡方程式，即∑Y=0和∑M_A=0，即挡土结构前后侧合力为零和挡土结构底端自由。由∑Y=0，得

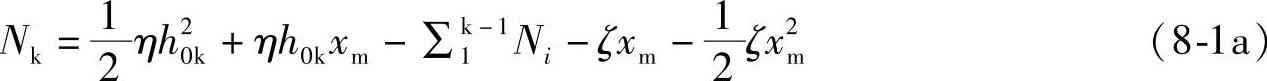
根据∑M_A=0和式（8-1a）得

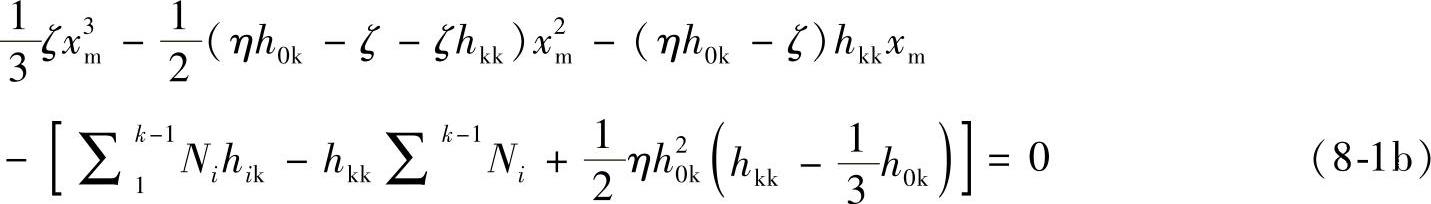
近似解的计算步骤如下：

（1）在第一次开挖中，式（8-1a）和式（8-1b）的下标k=1，而且N_i取为零，从式（8-1b）中求出x_m，然后代入式（8-1a）求得N_i。

（2）在第二次开挖中，式（8-1a）和式（8-1b）的下标k=2，而且N_i中N₁已知，N_k即为N₂，从式（8-1b）求出x_m，然后代入式（8-1a）求得N₂。

以此类推求得各道横撑轴力之后，求得挡土结构内力。

解析方法的共同特点为：

（1）力学模型简单，仅用静力平衡方程就能求解其内力，因此适合于工程界的应用。

（2）不能计算开挖时支撑轴力和挡墙内力的变化，因此将此类方法应用于支撑道数较多的挡墙结构时所得的结果明显偏大，且支撑道数越多，内力值越大。因此，这类方法仅能用于1～2道支撑的挡土结构。