深基坑围护设计与实例解析：古典方法优点及特点

围护墙结构的内力及变形计算的古典方法计算思路为：通过引入假设，将原本较为复杂的问题简化为静定问题进行计算。

其中悬臂式挡土结构的计算方法较为简单，可直接按静力平衡条件确定；自撑式挡土结构内力有很多种计算方法，如：适用于底端自由支承的单锚式挡土结构和悬臂式挡土结构的平衡法（亦称自由端法）、一般适用于底部嵌固的单锚式挡土结构的弹性曲线法（对底端自由支承的单锚和无锚挡土结构，其图解法的原则同样适用）及假想铰法（亦称等值梁法）。

等值梁法的计算原理为：对于有支撑或有锚杆的挡土结构，其变形曲线有一反弯点Q，如图8-8a、b所示。要求解此挡土结构的内力，有三个未知量：T、D和E_p2，而可以利用的平衡方程式只有两个。假想铰法是先找出挡土结构弹性曲线反弯点Q的位置，认为该点的弯矩为零，于是可把挡土结构划分为两段假想梁，上部为简支梁，下部为一次超静定结构，如图8-8b所示，这样就可以求得挡土结构的内力。

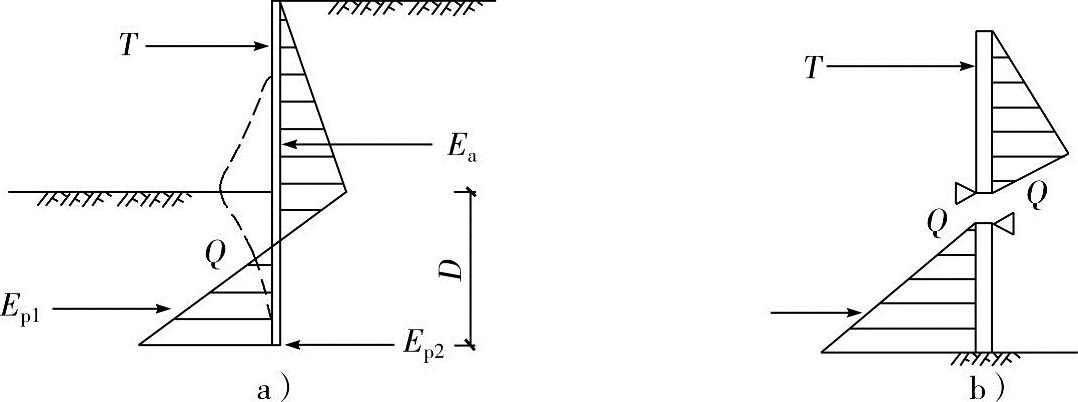
图8-8

a）挡土结构底端为嵌固时的稳定状态 b）等值梁法计算简图

采用假想铰法可以求解多支撑（锚杆）挡土结构内力，其关键问题在于假想铰Q点位置的确定，在这方面有以下几种理论及假定：

（1）假定假想铰的位置即是土压力为零的一点。

（2）假定假想铰为挡土结构入土面的一点。

（3）假定假想铰的位置为离入土面距离为y的一点。该y值由地质条件及结构特性决定，一般y=（0.1～0.2）H，如图8-9所示。

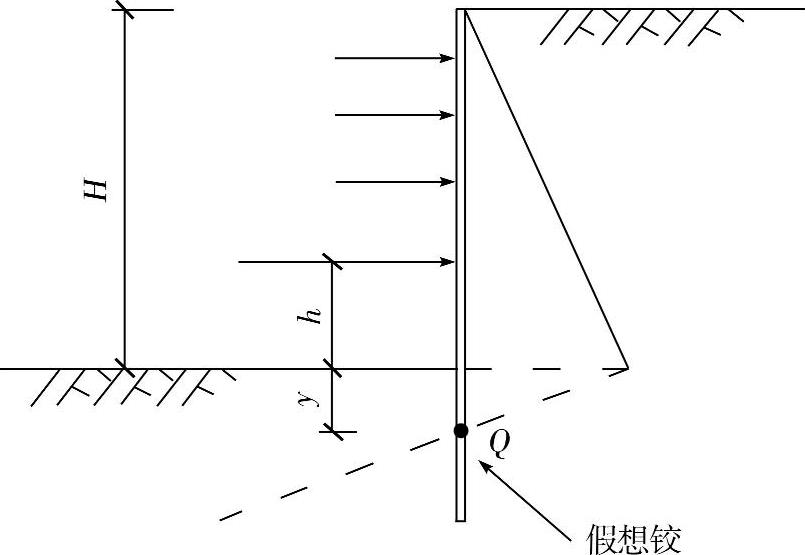
图8-9 多支撑挡土结构假想铰位置(www.xing528.com)

（4）假想铰的位置可按表8-1采用。

表8-1 多支撑挡土结构假想铰位置

等值梁法一旦确定出假想铰的位置，挡土结构的弯矩、剪力和支撑轴力即可按照弹性结构的连续梁法求解。

古典方法有如下特点：

（1）土对结构的作用简化为已知的荷载，故计算过程比较简单。

（2）所采用的土压力实际是土体处于极限状态时的土压力。但实际上，在目前结构设计由强度控制转向变形控制的情况下，土压力极限状态很难达到。此外，也无法考虑结构形式及刚度对土压力的影响。

（3）为使问题可以求解所引入的一些简化并无理论依据（如等值梁法中的假设，多撑计算中水平支撑力不随开挖变化等）。

（4）无法得到支护结构的变形及基坑外土体的变形。

（5）荷载—结构法在计算时对实际结构的受力作了较多的简化，较适用于形式简单的支护结构。