深基坑围护设计及实例解析中的稳定性分析成果

基坑支护体系整体稳定性验算的目的就是要防止基坑支护结构与周围土体整体滑动失稳破坏，它在基坑支护设计中是需要经常考虑的一项验算内容。

1.整体稳定性分析的条分法

当基坑周围场地空旷，环境条件允许时基坑坑壁可采用放坡开挖的形式。边坡稳定分析中比较常用的是基于极限平衡理论的条分法。条分法分析边坡稳定在力学上是超静定的，因此在应用时一般对条间力要作各种各样的假定，由此也产生了不同名称的方法，各种方法比较见下表2-2。

表2-2 几种条分法比较

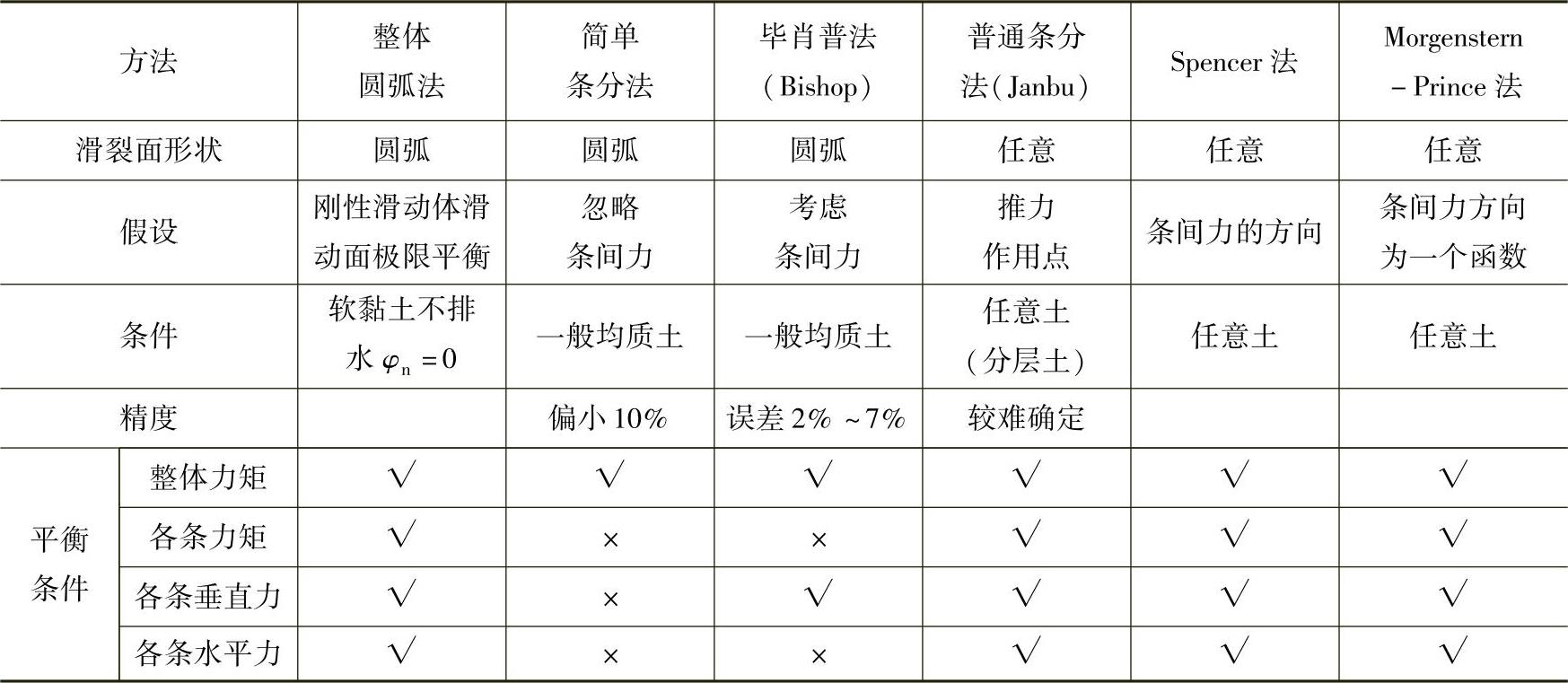
条分法可作如下概括：

（1）传统的瑞典圆弧滑动法在平缓边坡和高孔隙水压情况下进行有效应力法分析边坡稳定性时非常不准确，所计算的安全系数太低；此法的安全系数在“φ=0”分析中是相当精确的，而在采用圆弧滑裂面的总应力法分析时也是比较精确的。此法不存在数值分析问题。

（2）简化毕肖普（Bishop）法在所有情况下都是精确的（除了遇到数值分析问题情况外）。其缺点在于滑裂面仅为圆弧滑裂面以及有时会遇到数值分析问题。如果使用简化毕肖普法计算获的安全系数比由瑞典圆弧法在同样的圆弧滑动面上计算的安全系数小，那么可以推定毕肖普法中存在数值分析问题，在这种情况瑞典圆弧法的计算结果要比毕肖普法的计算结果更可靠。鉴于此，同时采用瑞典圆弧法和毕肖普法进行计算并比较是一个合理的做法。

（3）仅使用力的平衡而不考虑力矩平衡的条分方法，其计算结果对所假定的条间力方向极为敏感，不合适的条间力假定将可能导致安全系数出错。这类方法同样存在数值分析困难问题。

（4）满足全部平衡条件（力、力矩）的方法，在任何情况下都是精确的（除非遇到数值分析问题），这些方法计算的计算结果误差不超过12%，相对于可认为是正确的结果的误差一般不会超过6%。不过所有这些方法都存在数值分析问题。

2.具体设计计算方法

瑞典圆弧滑动条分法由于仅能满足整个滑动土体的整体力矩平衡条件，而不满足其他平衡条件，由此产生的误差一般会使求出的安全系数偏低10%～20%，而且随着滑裂面圆心角和孔隙压力的增大而增大，但此法应用的时间很长，积累了丰富的工程经验，一般得到的安全系数偏低（即偏于安全），故目前仍然是工程中常用的方法。具体计算方法详见各章相关部分。

3.整体稳定性分析数值分析方法

稳定问题是岩土工程经典问题之一，但由于岩土材料的非均匀性，影响因素的复杂性，很难通过某种理论方法得到极为精确的解答。因此许多学者从力学、地质学等角度出发对该问题进行研究，希望能够得到近似精确的解答。1952年，Drucker和Prager首次把静力场和速度场结合起来，并通过极值的方法求解，但未及时地建立岩土体极限分析法。1975年，Chen和Liu系统地提出岩土体极限分析理论。

由于极限分析方法避免了极限平衡方法的不合理假定与有限元方法的繁琐计算而具有精确性和简便性的特点，所以在岩土工程设计与计算中得到了广泛的应用。近几年来，随着数值分析手段的进步和计算机性能的提高，边坡稳定分析中出现了多块体上限方法、极限分析上下限有限元技术、强度折减有限元技术等新方法。

（1）极限分析方法。目前岩土工程工程稳定性问题分析的极限分析方法是以传统塑性力学的极限分析上下限定理为依据的。极限分析上下限定理的基本假定包括：①材料呈理想塑性，即不发生应变硬化或软化；②服从Drucker公设，屈服面外凸和服从关联流动法则；③小变形假定，故可应用虚功原理。应用虚功原理及关联流动法则，可得极限分析上下限定理的基本内容为：①下限定理：对于一个静力许可的应力场（在全局范围内满足平衡方程、应力边界条件和不违背屈服准则），与之对应的外荷载必小于或等于真实极限荷载；②上限定理：对于一个运动许可的速度场（满足相容条件和位移边界条件），根据外力功功率和内能耗散率相等确定的外荷载必大于或等于真实极限荷载。

一般来说，构造运动许可的速度场要比全局范围内的静力许可应力场简单得多，因此上限方法在实际中应用的更为广泛。此处只给出用于上限计算的能量方程。极限分析上限理论的叙述方法有许多种，此处采用一种比较简练的说法，即对于任何运动许可的破坏机构，内能耗散率不小于外力功功率，可表示为(www.xing528.com)

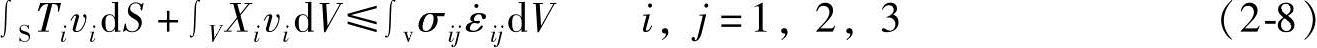
式中 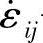——运动许可速度场中的塑性应变率场；

v_i——与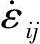满足几何相容的速度场（运动许可速度场）；

T_i、X_i——边界S上的面积分布力矢量和区域V内的体积力矢量；

σ_ij——通过关联流动法则与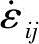相联系的应力场。

极限分析方法与现代数值分析手段相结合的应用主要有两类，一类为多块体上限方法，另一类为极限分析有限元方法。目前这两类方法在边坡稳定、地基极限承载力及挡土墙土压力等经典岩土领域稳定性分析问题中都有了较多的应用。

（2）强度折减方法。

1）强度折减有限元的基本原理。采用强度折减是有限元方法分析边坡稳定性的有效方法，它是在理想弹塑性有限元计算中将边坡岩土体抗剪强度参数逐渐降低直到其达到破坏状态为止，可以自动根据弹塑性计算结果得到临界滑动面，同时得到边坡的强度储备安全系数F。

早在20世纪70年代，Zienkiewicz就提出了采用降低岩土体强度的方法来计算岩土工程的安全系数，但受限于当时的计算条件，强度折减有限元方法并没有得到广泛的应用。近年来随着计算机软硬件的高速发展，特别是大型商业有限元软件的广泛应用，强度折减有限元技术成为边坡分析领域生命力十足的方法。

2）边坡稳定失稳判据。

应用强度折减有限元分析边坡稳定性的一个关键问题是边坡失稳的判据。目前的失稳判据主要有三类：①以广义塑性应变或等效塑性应变从坡脚到坡顶贯通作为边坡破坏的标志；②在有限元计算过程中采用力和位移的不收敛作为边坡失稳的标志；③以坡体或坡面的位移发生突变作为边坡失稳的标志。对于三种标准，郑颖人等（2005）研究后指出，土体滑动面塑性区贯通是土体破坏的必要条件，但不是充分条件。土体破坏的标志应是部分土体出现无限移动，此时滑移面上的应变或者位移出现突变，因此，这种突变可作为破坏的标志。此外有限元计算会同时出现计算不收敛。上述②、③两种判断依据是一致的。从计算结果来看判据①与判据②、③的差异也不大，因而采用有限元数值计算是否收敛作为土体破坏的依据是合适的。

3）强度折减有限元分析边坡稳定的实现过程。强度折减有限元法分析边坡稳定性可以分成以下3步：

①建立边坡的有限元分析模型。坡体各种材料采用不同的单元材料属性；计算边坡的初始应力场，初步分析在重力作用下，边坡的变化和应力；记录边坡的最大变形。

②增大F。将折减后的强度参数赋给计算模型，重新计算，记录计算收敛后的边坡最大变形和塑性应变发展情况。

③重复②步，不断增大F值，降低坡体的强度参数，直至计算模型不收敛，则认为边坡发生失稳破坏。计算发散前一步的F值就是边坡的安全系数。对于边坡①步计算就不收敛的情况，在进行②步和③步计算时，F应该逐渐减小，直至计算收敛、边坡重新稳定。