LSSVM多分类器自适应识别方法研究成果

1.LSSVM介绍

支持向量机（SVM）是由Vapnik等人基于统计学VC维理论和结构风险最小原理建立的一种机器学习方法[157]。该方法依据有限的样本信息，可在模型的学习能力和复杂性之间寻求较好的平衡，能较好地解决非线性、小样本、高维数与局部极小点等问题[158]。近年来，SVM已被广泛应用于分类与回归问题，被很多学者认为是一种较好的分类方法，其分类精度一般超过神经网络与决策树等分类方法[159]。

SVM模型的训练数据样本可描述为其中xi是样本的特征，yi是样本所属的类别。求解SVM模型的目的就是寻找区分两种样本类别的最佳分类超平面。超平面表达为公式（6-11）：

式中ω是超平面的法向量，x为超平面的一个点，b是偏离常数。图6-3为SVM模型示意图。SVM可通过合适的核函数将原始空间里线性不可分的输入向量映射到高维空间，进而在高维空间里求解最优分类超平面。

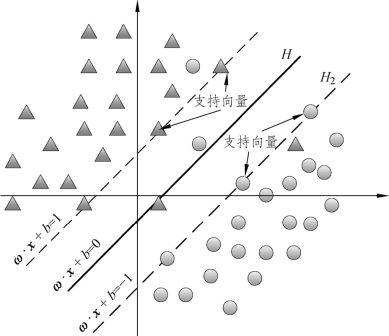
图6-3　SVM分类示意图

为了避免求解SVM模型中较为耗时的二次规划问题，Suykens等人改进了标准的SVM模型，提出了最小二乘支持向量机模型（least square support vector machine，LSSVM）。LSSVM模型中，以等式约束条件替代标准SVM模型中的不等式约束条件，提高了模型的求解速度和收敛精度[160]。假设某样本集为LSSVM模型输入数据，为LSSVM模型输出数据，则LSSVM模型对该样本集拟合的函数形式为

式中为一种将原始输入向量映射到高维特征空间的非线性函数，权向量，偏置量。

为了求解拟合函数，定义如下目标函数：

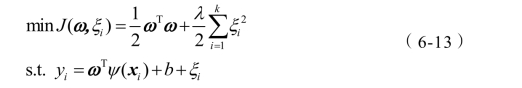
式中λ为惩罚系数，为松弛变量，构建拉格朗日函数：

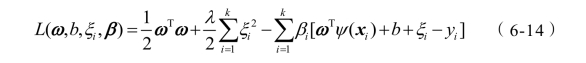
式中βi为拉格朗日乘子。

根据Karush-Kuhn-Tucker（KKT）条件有：

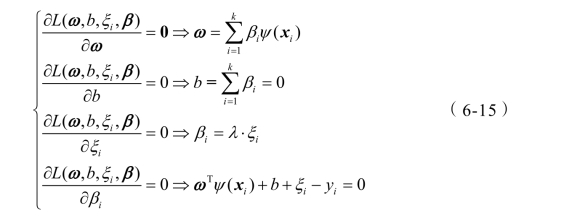
通过代入消元法消去ω和ξi，可得到目标函数优化问题的解析解：

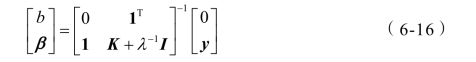
式中方阵K满足如下条件：

故求得的最小二乘模型为

(www.xing528.com)

式中为最小二乘支持向量机的核函数，是满足Mercer条件的任意对称函数。

常用的核函数有线性核、多项式核、S 型曲线核和高斯核。而高斯核函数，又称为径向基核函数RBF，具有较好的统计能力。因此，本节选用高斯核函数，用如下式子表达：

式中x与分别是原始特征空间的输入数据与高维特征空间的输入数据，g为RBF核函数的半径。

2.参数优化

如上部分所示，核参数g与惩罚系数λ是LSSVM模型的两个重要参数，能显著影响模型分类的准确率。为了提高模型分类的准确率，本部分运用粒子群优化（particle swarm optimization，PSO）算法对这两个模型的参数进行优化。PSO算法由Kennedy[161]等人在1995年首先提出，是一种基于种群的随机优化方法，即通过种群内个体之间的竞争与合作来完成优化求解。这种算法具有精度高、收敛快且实现容易等优点，逐渐在实际问题的解决过程中展示了其优越性。

关于PSO算法，其核心思想是通过所有粒子在追随当前已寻找到的最优值的过程中来搜索其全局最优值。假设PSO算法的潜在解为一群粒子，在算法初始化时，每个粒子都被赋予一个随机的速度和位置，并在一定的维度空间里移动。对于每个粒子，其目标是到达一个最佳位置点，而且所有粒子均记录其到达的最佳位置点。例如，第 i 个粒子到达的最佳位置点记为PLi，而在所有PLi中最佳的位置被定义为全局最优值，记为PG。每个粒子在一定维度的搜索空间内以某一速度移动，此速度可依据其自身的移动经验和周围同伴的移动经验来动态调整其下一步的移动方向和大小，其迭代示意图如图6-4所示。

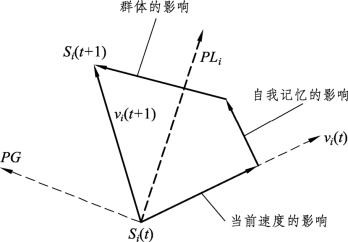
图6-4　PSO算法原理示意图

在每一次的更新过程中，每个粒子的速度和位置按公式（6-20）和（6-21）进行迭代：

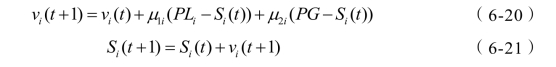
式中i为粒子序号，t为时间序号；vi是第i个粒子的速度，Si是第i个粒子的位置；PLi为第i个粒子能达到的最优位置，PG是全部粒子发现的最优位置；μ1i和μ2i为0与1之间的随机数。依据本书实验数据特点，第i个粒子的移动速度可转化成公式（6-22）：

式中τ（t）为惯性函数，γ1和γ2为第i个粒子t时刻的加速度。

3.多分类方法

由上部分可知，标准的LSSVM分类器是一个2类分类器，而本书要处理的是多种驾驶愤怒强度的识别问题，因此，需要将2分类的LSSVM分类器推广到M0类分类器。设训练集中样本所属类别yi共有M0个取值，即，因此，通过构建多分类的LSSVM分类器即可求得其决策函数f（x），使得f（x）能将所有样本划分为M0类。

目前，基于SVM的多分类应用的实现常常基于组合编码或多目标优 化[162-164]。由于多目标优化方法需要求解变量的个数较多，且求解步骤较为烦琐[163]，因此，本部分将采用组合编码方法，即构建多个LSSVM分类器，来实现多分类问题的求解。目前，有一对一编码、一对多编码、最小输出编码（minimal output coding，MOC）和纠错输出编码等常用组合编码方法。其中，MOC方法只需要构造最少数目（N1）的2分类LSSVM分类器就可实现对M0类样本的分类。此外，MOC方法具有计算量较小且较易实现等优点，本部分将采用该方法来求解LSSVM模型的多分类问题[163]。

在对M0类样本进行分类时，针对每一类别i，MOC赋予其唯一的编码：

式中n=1，2，…，Nl；yin∈{1，-1}，分别代表正类和负类，那么MOC的输出位数Nl可用公式（6-24）计算：

式中Nl表示MOC方法需要建立的2分类LSSVM分类器的数目为大于或等于log2M0的最小整数。Nl个独立的LSSVM分类器的分类结果可组成l个码字s0，然后求解s0与M0个编码间的汉明距离（hamming distance，HD）[165]，具有最小HD的类可被认为拟测样本的类别。