样本熵计算原理，详解及应用方法

ECG信号作为自主神经系统活动的外在表现，在不同的心理状况下呈现不同的表现特征。正常情绪下，心脏搏动较为规律，心电波复杂性较低；而当遇到突发、刺激事件造成紧张或情绪波动等状况下，心脏搏动（心率波动）的随机性较大，心电波的复杂性会增大。而样本熵是一种度量时间序列复杂性的非线性动力学参数，通常采用一个非负数表示，它能反映时间序列中新信息的产生率。时间序列越复杂，样本熵值越大。目前，在医学等相关研究中，心电、脑电信号的样本熵分析方法已经取得了很好的效果。因此，为了准确描述ECG信号在不同驾驶愤怒状态下的变化规律，本书运用样本熵方法来提取ECG信号特征。

样本熵是一种评价时间序列规则度或复杂度的算法，由Richman等人对近似熵改进而得。它对脑电、心电、肌电等非线性动力学时间序列具有很好的适用性。样本熵具有较好的抗干扰与抗噪能力，运算时间较短，且较短的数据可达到有效分析的目的[136]。样本熵可用SampEn（m，r，N）表示，其算法定义描述如下：

首先，设有N个数据组成的连续时间序列{w（j）：1≤j≤N}，用此时间序列w（j）构造N-m+1个m维向量{Xm（i）：1≤i≤N-m+1}，其中m为每个向量的维数，即

同理，构造（N-m）个（m+1）维向量{Xm+1（i）：1≤i≤N-m}，即

定义任意两个向量之间的距离为

设Bi在相似性容限 r 下，满足的数目，1≤i≤N-m，1≤j≤N-m ，有

其中表示在相似性容限r的限制下，N-m个与一个相似的概率。(www.xing528.com)

其次，将维数加1，变成m+1，重复上述公式（4-8）至公式（4-11）的过程，得到。

最后，对所有的Bim（r）取平均值，记作Bm（r），为

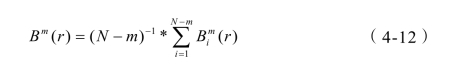
那么

因此，对于有限样本量为N点的时间序列，样本熵计算公式为

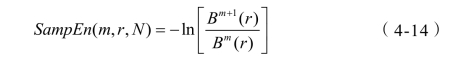
根据上述样本熵的计算原理描述，其计算流程如图4-3所示。

图4-3　样本熵计算流程图

样本熵SampEn（m，r，N）的值与参数m，r和N的选取有关，不同的嵌入维数m和相似容限r，对应的样本熵也不同，它们是样本熵计算过程中的两个重要参数。一般情况下，当m =1或2时，r=0.1～0.25SDx（待求样本熵数据序列的标准差），计算得到的样本熵具有较为合理的统计特性[137]。本书试验了30组m和r值，以不同愤怒强度下的心电样本熵值的显著性差异作为评价指标，得到了最优的组合值为m=2，r=0.2。