线性回归置信区域研究成果

郝尔西博士在讲到水位流量关系曲线时,曾经引用公式计算了置信区域。他给出的公式包括:曲线的不确定度百分数的公式

以及曲线上任意一点不确定度百分数的公式

上述各式中H为水位,a为断流时水位,其值为负。Qc为给定的H由回归曲线上查出的流量。而式(27)中的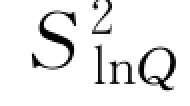为

式(30)中的Se可用Se,1、Se,2、Se,3任取一个代入,至于Sm,r郝尔西称为平均值的(相对)标准差,但是从意义上看它是水位为H所对应的Q的(相对)标准差,XSm,r则为该点的置信区间长度的一半,至于tα,他建议取为2,于是当n已知后即可由自由度为n-2的t分布查出tα=2的置信率,将不同H所对应的Q的置信区间定出后,并将其联接,即得整个水位流量关系曲线的置信区域。郝尔西博士举了一个例子,并且采用Sm,r=Se,3SH绘出了置信区域。有了这样的区域,对于评价整个水位流量关系曲线的精度是较全面的,但是他的有些提法及在公式上的应用上,有不够清楚和值得推敲的地方。现在根据回归分析的有关结果扼要阐述于后,作为对他讲课的一种补充。

大家知道水位流量关系一般可以写成

对于式(31)取对数

引进简化表示

则式(31)为

设Y的分布为正态分布,即

且(www.xing528.com)

此时的回归问题称为一维正态线性回归。现采用下述统计量

此处

Y,X值代入,利用前面的表示

从而置信区间为

所对应的Q置信率为

将所得的结果式(43)、式(41)及式(42)等与郝尔西博士给出的对比后,可以看出几点:第一,他在确定Sm,r中的Sl时平行地引进了包含在式(27)、式(28)、式(29)3种Se,1、Se,2、Se,3公式,并用例子说明这3个公式给出的结果是相同的。但从上面的推导看,正确的做法应该是Sm,r=Se,2SH。至于这3个公式是否等价问题,还没有看到其证明。第二,按其意义而言,郝尔西博士给出的Se是整个回归线的标准差,它表示给定回归的准确程度,Sm,r是曲线在任意点的标准差。

知道了水位流量关系上任意一点的不确定度,则推算的日平均量的不确定度就不难了。事实上由式(31),求得日平均流量的不确定度百分数为

其中X(H+α)表示水位不确定度百分数,XC表示公式(31)中的C的不确定度百分数。在水位一定(准确的)条件下,由于XC引起的流量变幅在±Sm,rQc,故XC的不确定度百分数就是XSm,r,所以