山尼洪公式，在水文测验理论问题研究中的应用

安芸皎一在流量测定法[3]中推荐山尼洪公式可以用于水下悬索的偏角改正。山尼洪公式是取悬索曲线为悬链线而得到,推导如下。山尼洪公式只考虑了铅鱼在河底的情况。如采用图17所示的坐标系x'o'y',则曲线的坐标方程为

图17　悬链线(山尼洪公式)示意图

曲线长的方程为

但是为了便于比较起见,将其换算到前面采用的坐标系xoy,则

此处sh及ch为双曲线正弦和余弦,之前从未见过山洪尼公式对水下悬索曲线适宜性的最初推导,看来是直接借用悬链线的结果,但是早在文献[10]就指出其推导过程,因为既然是假定为悬链线,则必须假定单位湿绳长所受的阻力相等,以及忽略了铅鱼的阻力,设单位湿绳长的阻力为q,则悬索曲线的方程为(图17)

由于当y=0时,l=s1,故

故式(111)为

对此式微分得

即

积分后得

其中

再对式(115)积分,并代入条件x=0,y=0,则有

注意到y=H时,x=xc,故

于是式(120)又可写成

并且式(120)给出了确定参数a的方程。对比式(108)与式(121)、式(109)与式(117),可见完成了山尼洪公式的推导。

至于山尼洪公式给出的改正数,可以从式(116)得到

后一式就是日本安芸皎一在其所著的《流量测定法》[3]推荐的山尼洪的偏角改正公式,也是国际标准(ISO3454)[9]所采用的。

我国李萼奇曾独自提出[5]

我国李萼奇当时未见到山尼洪公式,因而未研究他们公式的异同,笔者曾最早指出[10]他们俩人的结果是完全恒等的;这一点只需要注意对数函数与双曲线函数之间关系就明确了。事实上,如令

则(www.xing528.com)

即

因此式(125)为

再将式(124)代入,则有

此即山尼洪公式。

那么山尼洪将悬链结果搬用至水下悬索曲线在理论上是否有什么根据?也就是说如果单位湿绳长所受阻力相等,它对应什么样的流速分布?这种流速分布在河流中是否有可能出现?现在考虑微元dy上悬索所受到的阻力dP1。按照山尼洪公式假定,并注意到式(113)之后,有

此处微元ds、dL均与微元dy对应,并且由图14可知,当y增加时,s=s1L增加,L减小,再将式(115)代入上式,则有

另一方面,由流体力学知作用在dy上的阻力为

从式(129)、式(130)得到

当y=H时,V=V1于是

此处V1表示河底流速,而当y=0时,V=V0,于是

式(133)可改写为

将式(132)、式(134)代入后,则有

即

表11　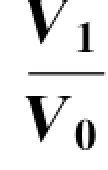与k1关系

图18　山尼洪公式对应的流速分布

相应的山尼洪公式对应的流速分布见图18,而改正数误差则见表12,流速分布式(136)一般经验相反,是很不合理的,这表现在:第一,曲线居然凹向下游,而不是凸向下游;第二是底部速度与最大速度之比太大,如果按抛物线流速分布,当平均流速与水面流速之比k1=0.855时,河底流速与水面流速之比=0.565,而此时表11却为0.78;第三,从式(34)看出流速分布流速参数本身又与s1、H、tanα1、λ1有关,或与tanα1、λ1有关,这也是不合理的,总之从理论上看,山尼洪公式是没有理论根据的,只是简单地搬用悬链线至水下。

由于山尼洪公式既然缺乏理论根据,又忽略了铅鱼阻力,因此难以想象它的相对改正数会在较宽的范围内符合实际。表12给出了经过大量实测资料检验的理论公式(80)与山尼洪公式算出的相对改正数的对比,可见偏角α1＜30°山尼洪公式误差较小,当40＜α1≤50°,引起水深的误差超过1%,而当α1≥70°,引起水深的误差更大。可见,除非偏角很小,否则没有适用意义,特别是它更不能运用到铅鱼不在河底的情况。

表12　山尼洪公式改正的误差(α1=0°)