相对改正数：铅鱼落床效果

将式(43)代入式(79),注意到此时ηc=1,得到相对改正数为

其中α'1由式(46)给出,即

而

称为悬索的拉紧度,将式(91)代入式(90),则有

经过数字计算,按式(93)编写成了改正表,见表8。从表8中看出当α'1固定,随着拉紧度μ0的减小,λ也减小。其实拉紧度相同在α'1为40°,当拉紧度为0.500,α0=2°时,则tanα1=0.500tanα'1,即α1为22.7°。可见如果α'1=40°,当μ0=1,则初始的偏角为α=400;而按前述当铅鱼落于河底,如μ=0.5,则初始偏角仅22.7°,显然前者的改正数λ大于后者。

表8(一)　铅鱼落于河底的相对改正数

续表(www.xing528.com)

表8(二)　铅鱼落于河底的相对改正数

续表

表8(三)　铅鱼落于河底的相对改正数

为了具体了解这种条件改正数的情况和它与铅鱼趋近于床面改正数的差别,我们再举出前面提到的例子(图9)当k1=0.85,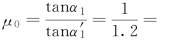0.833,α'=50°时,求出α'0=-7.1°,λ1=0.1309。而如果铅鱼只趋近于床面,则tanα=0.833,tan50°=0.933,即α=44.8°,相应的λ1=0.1157。可见两者有一定差别。另一方面经过进一步对比这两种情况下(表4和表7)的相对改正数得到,当α＜40°,悬索的放松度μ0≥0.95时,两者的差别基本可以忽略。

从上述结果可看出,在用铅鱼量测水深时,为了避免难于掌握的铅鱼趋近于床面但不落于河床的极限状态,可以采用两种方法:当偏角不是很大时,可直接使铅鱼落于河底,但控制拉紧度μ0＞0.95,测其湿绳长及偏角,并按铅鱼趋近于河底的相对改正数进行改正;当偏角很大时,应先大体按趋近于河底情况测定α1、s1,然后适当放松,测定α1、s1,再分别据k1、α0、α1、s1,由表4进行改正和根据α0、k1、α'1、μ0,s'1由表7进行改正,求出水深后再平均。由于采用两个数平均,此时铅鱼是否恰好趋近于河底的影响就小了,因此不仅可以适当节省调整铅鱼恰趋于河底的极限状态的时间,而且精度也能保证。