1.地球的形状和大小
为了确定地面点位,就需要相应的基准面和基准线作为依据,测量工作是在地球表面进行的,所以测量工作的基准面和基准线就与地球的形状和大小有关。
地球的自然表面是很不规则的,其上有高山、深谷、丘陵、平原、江湖、海洋等,最高的珠穆朗玛峰高出海平面8 844 m,最深的太平洋马里亚纳海沟低于海平面11 022 m,其相对高差不足20 km,与地球的平均半径6 371 km相比是微不足道的,就整个地球表面而言,陆地面积仅占29%,而海洋面积占71%。
因此,可以设想地球的整体形状是被海水所包围的球体,即设想将静止的海水向整个陆地延伸,用所形成的封闭曲面来代替地球表面,如图1-1所示。此封闭曲面称为大地水准面。由大地水准面所包围的形体称为大地体。通常用大地体来代表地球的真实形状和大小。研究地球的形状和大小,就是研究大地水准面的形状和大地体的大小。
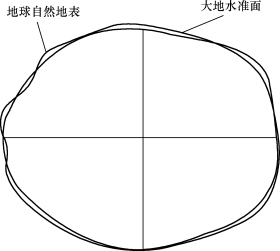
图1-1 地球自然表面
水准面的特性是处处与铅垂线垂直。水准面和铅垂线就是实际测量工作所依据的面和线。地球内部质量分布不均匀,致使地面上各点的铅垂线方向产生不规则变化,所以,大地水准面是一个不规则的无法用数学式表述的曲面,在这样的面上是无法进行测量数据的计算及处理的。因此人们进一步设想,用一个与大地体非常接近的又能用数学式表述的规则球体即旋转椭球体来代表地球的形状。如图1-2所示,旋转椭球体的形状和大小由椭球基本元素确定,即长半轴a、短半轴b、扁率α。其是由椭圆NESW绕短轴NS旋转而成的。
![]()
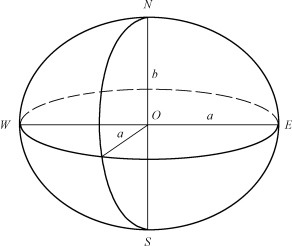
图1-2 旋转椭球体
一个国家或地区为处理测量成果而采用与大地体的形状大小最接近,又适合本国或本地区要求的旋转椭球体,这样的旋转椭球体称为参考椭球体。确定参考椭球体与大地体之间的相对位置关系,称为椭球体定位。参考椭球面只具有几何意义而无物理意义,它是严格意义上的测量计算基准面。
我国1954年北京坐标系采用的是克拉索夫斯基椭球,1980年国家大地坐标系采用的是1975国际椭球,而全球定位系统(GPS)采用的是WGS-84椭球。(https://www.xing528.com)
由于参考椭球体的扁率很小,在小区域的普通测量中可将地(椭)球看作圆球,其半径R=(a+a+b)/3=6 371 km。当测区范围更小时,还可以将地球看作平面,使计算工作更为简单。
2.地面点竖向位置
一个点的位置需要用三个相对独立的量来确定。在测量工作中,这三个量通常用该点在参考椭球面上的铅垂投影位置和该点沿投影方向到大地水准面的距离来表示。其中,前者由两个量构成,称为坐标;后者由一个量构成,称为高程。也就是说,用地面点的坐标和高程来确定其位置。
3.高程系统
(1)绝对高程。在一般的测量工作中都以大地水准面作为高程起算的基准面。因此,地面任一点沿铅垂线方向到大地水准面的距离就称为该点的绝对高程或海拔,简称高程,用H表示。如图1-3所示,图中的HA、HB分别表示地面上A、B两点的高程。我国规定以1950—1956年青岛验潮站多年记录的黄海平均海水面作为我国的大地水准面,由此建立的高程系统称为“1956年黄海高程系统”。新的国家高程基准面是根据青岛验潮站1952—1979年的验潮资料计算确定的,依此基准面建立的高程系统称为“1985年国家高程基准”,并于1987年开始启用。
(2)相对高程。当测区附近暂没有国家高程点可联测时,也可临时假定一个水准面作为该测区的高程起算面。地面点沿铅垂线至假定水准面的距离,称为该点的相对高程或假定高程。如图1-3中的H'A、H'B分别为地面上A、B两点的假定高程。
相对高程系统和黄海高程系统联测后,就可以推算出相对高程系统所对应的假定水准面的绝对高程(H0),进而将地面点的相对高程换算绝对高程,也可以将绝对高程换算为相对高程。显然地面点A的换算关系为

在建筑工程中,又将绝对高程和相对高程统称为标高。
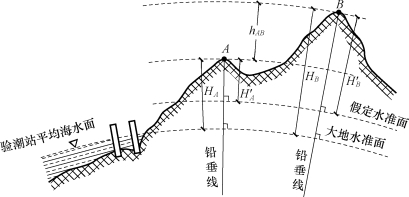
图1-3 绝对高程与相对高程
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




