钢桥失效事故分析：拱肋局部稳定性探讨

主拱钢圆管截面名义半径为r，厚度为t，钢管内外流体压力为p（以背向圆心为正），侧向荷载作用下变形的圆管截面的等效半径为r0=r/（1−3a/r ），变形量为a=（Dmax−Dmin ）/4，但a≤0.1r，如图13.9所示，Gresnigt[10]公式的临界屈曲应变εcr为：

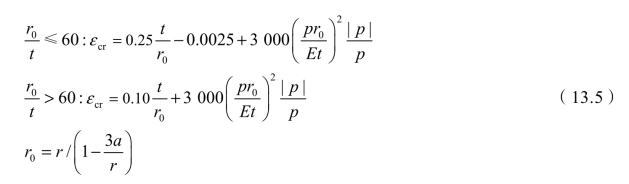
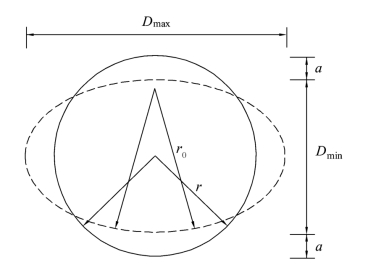
图13.9　圆管截面变形

根据式（13.5）可见，阿摩尔桥主拱空心钢管（p＝0，r/t＞60）的临界屈曲应变可简化为：

由此可见，钢管径厚比（r/t）及截面变形量（撞深）a对局部屈曲临界应变影响很大。径厚比基本上与临界屈曲应变（应力）成反比；当钢管径厚比不变时，截面变形量（撞深）a由撞击力和撞击接触面积确定，极大影响临界屈曲应变（应力）。

采用ANSYS建立主拱钢管节段（长度为L，原桥结构取相邻立柱间距离L＝30 m，钢管厚度保守取为 18 mm）空间有限元非线性模型，不考虑横撑和加劲肋，节段两端限制横向位移，轴向施加23 400 kN轴力。根据船桅一般尺寸和撞击后船桥密贴接触原则，节段中间横向施加船撞力，加载面积（轴向×径向）为矩形（2 m×2 m），钢管采用Shell43单元，如图13.10。Q345钢材应力应变关系仍为理想弹塑性模型，E＝210 000 MPa。

图13.10　主拱节段有限元模型

1.受力及稳定性分析

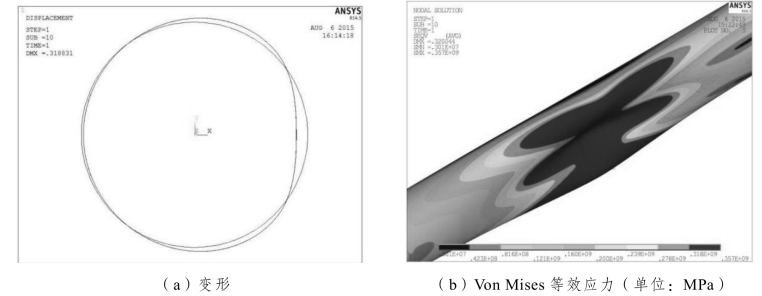
根据主拱节段有限元模型，得到截面的最大变形和Von Mises等效应力，如图13.11。结果表明：局部结构变形主要是钢管截面形状变形，弯曲变形很小，可忽略不计。撞击区域钢管附近约 3.6 m×6 m区域钢材达到屈服，a＝0.15 m。根据式（13.6），可得到临界应力为σcr=Eεcr=151.8 MPa ，小于屈服强度345 MPa。

分别对厚度为 15 mm、18 mm 和 20 mm 的钢管分析截面最大横向位移和荷载之间的关系，如图13.12所示。当荷载达到一定值，如2 000 kN时，钢管开始出现非线性行为，且厚度越小，钢材屈服越早出现，截面刚度减小了。通过图13.11和13.12可见，船撞力对钢管结构的受力影响很大，主要体现在两个方面：① 撞击造成的截面变形降低了临界屈曲应力（抗力）；② 形成的钢管局部屈服区削弱了截面承载面积，增加了拱轴向应力（作用效应）。

(www.xing528.com)

图13.11　截面变形及Von Mises等效应力

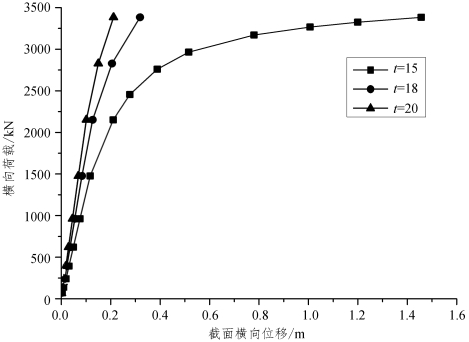
图13.12　管截面横向位移-荷载曲线

2.关键影响参数分析

（1）关键结构参数。

基于原桥主拱截面，研究关键结构参数，如钢管长径比L/r和径厚比r/t对钢管截面横向变形的影响，结果如图13.13所示。

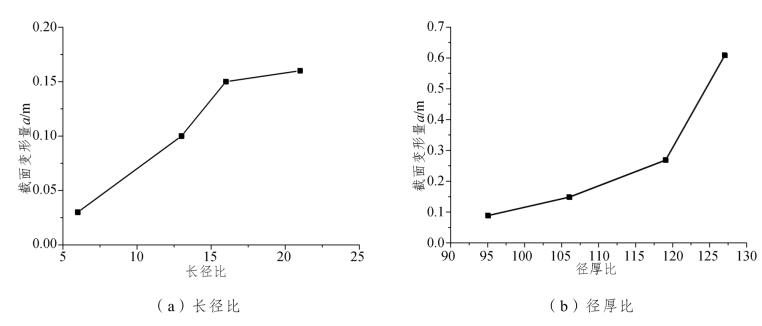
图13.13　关键结构参数对截面变形量的影响

钢管长径比L/r越大，船撞作用下钢管屈服范围越大，截面变形量a随之增加，根据式（13.6），局部临界屈曲应变减小。长径比L/r还可看作钢管环向加劲肋布置间距的量度，增加环向加劲肋可以有效提高钢管稳定承载能力。同理，径厚比与临界屈曲应变成反比，是关键的截面设计控制因素。

（2）船撞力。

船撞力包括荷载值和撞击接触面积，对钢管截面变形（撞深）及临界屈曲应力影响很大。由式（13.6）和有限元模型，得到实桥钢管节段（L＝30 m）不同撞击接触面积（轴向×径向）分别为 2 m×2 m、1 m×2 m、1 m×1 m时对应的截面变形和临界屈曲应力关系曲线，如图13.14。

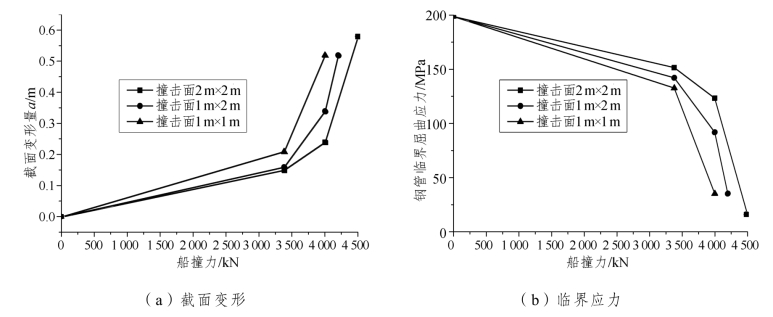
图13.14　船撞力对钢管截面变形记临界应力的影响

结果表明：船撞力大小和撞击面积对于截面变形量 a 和临界屈曲应力影响很大。撞击接触面积越小，截面局部变形（撞深）越大，撞击荷载越大，临界屈曲应力下降也越快。