箱梁顶板为受压加劲板，根据欧洲规范[8]，对宽度为 b、厚度为 t、横肋间距为 a、纵肋间距为 b1 的加劲钢板，其屈曲模态分为类板（plate-like）模态和类柱（column-like）模态，如图7.4所示，对应的弹性失稳临界应力计算理论如下：
1.类板屈曲临界应力
对于四边简支的均匀受压板，其弹性屈曲临界应力σcr可用式（7.1）计算：
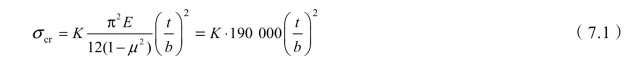
式中：E和 μ 为钢板弹性模量和泊松比，t和b为板件厚度和宽度，弹性屈曲系数K可按以下两种情况计算：
（1）对于无纵向和横向加劲肋的四边简支板来说，其弹性屈曲系数K可由边界条件保守取值为：四边简支K值为4；三边简支，一边自由时K值为0.43。
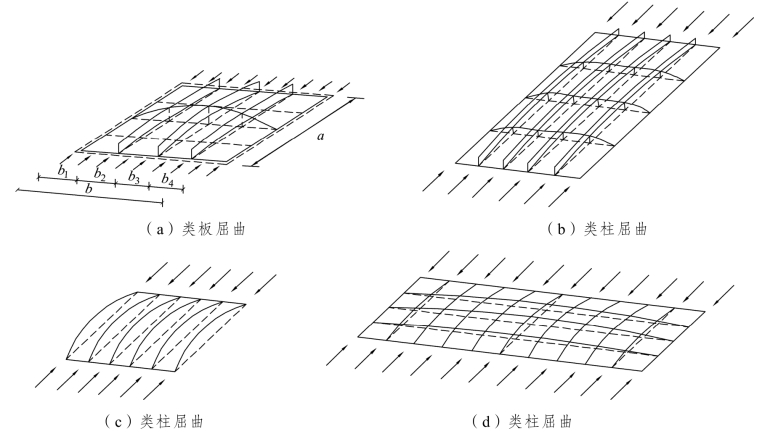
图7.4 受压加劲板屈曲模态分类[8]
（2）对于纵向加劲肋等间距布置的加劲板弹性屈曲系数K，基于正交异性板等效原则，可由式（7.2）计算：
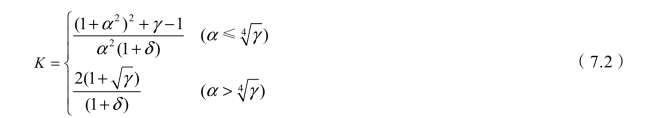(www.xing528.com)
式中：γ=∑Is1/I p ；δ=∑As1/Ap；α=a/b ≥0.5；Is1、Ip （=bt 3/10.92）及As1、Ap分别为单个加劲肋和加劲板的惯性矩和面积。
2.类柱屈曲临界应力
对于类柱屈曲，把加劲板的屈曲等效为T形截面（由加劲肋及其周围加劲板组成）的柱子的屈曲，临界屈曲应力σcr为：
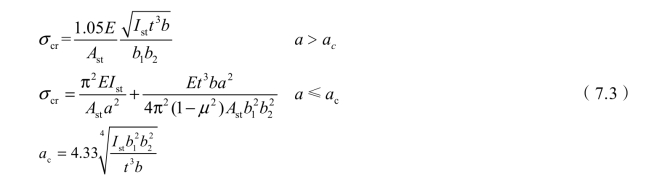
式中：Ist和Ast分别为 T 形截面（被加劲板宽取加劲肋两侧b1/2和b2/2）的惯性矩和面积；a为横向加劲肋间距，如图7.5所示。
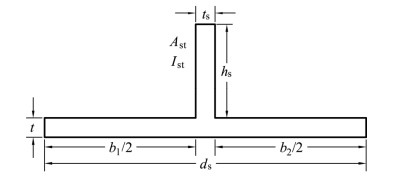
图7.5 T形截面
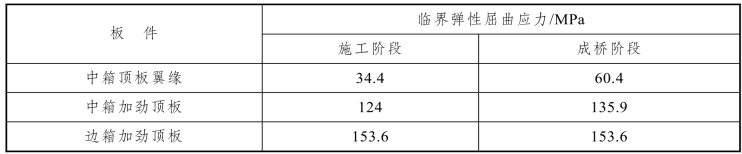
根据公式（7.1）～（7.3），可得到板件的弹性临界屈曲应力。由于弹性临界屈曲应力没考虑初始缺陷和残余应力，其值偏大。按理论模型对西门大桥关键板件进行分析，得到施工阶段和成桥阶段的临界弹性屈曲应力，如表 7.1 所示。由于约束条件差异很大，施工阶段中箱顶板翼缘的屈曲应力只有成桥阶段的一半左右，而且偏小，导致施工阶段自重作用下翼缘屈曲变形，形成高差，如图7.3（a）所示。而且根据原桥设计和欧洲规范，加劲顶板均为类柱屈曲，一旦失稳，即失去刚度。
表7.1 顶板临界弹性屈曲应力
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
