塔科马大桥的垮塌主要原因是扭转失稳,而扭转失稳机理的关键在于H型加劲梁横截面上大型旋涡的形成以及旋涡沿桥梁横截面的移动,如图5.7所示[8]。
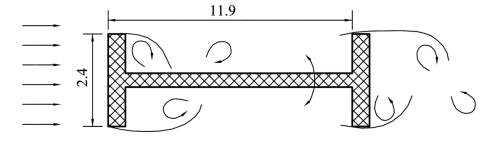
图5.7 加劲梁上旋涡的移动(单位:m)
Larsen[9]采用宽高比为5∶1的简单H型断面,建立了一个简单的分析模型研究扭转失稳机理,假定如下:
(1)假定加劲梁截面扭转振动的形式为正弦曲线,其无量纲周期T=U/fB,其中f为扭转频率。
(2)气动力做功W=Fv,其中F为旋涡产生的升力,v等于F作用点处梁的振动速度。旋涡总功等于一个周期内所有旋涡做功的积分。
(3)旋涡产生的升力在旋涡漂移过程中保持恒定。
(4)旋涡的无量纲移动时间与弹性悬吊横截面的振动周期无关。(https://www.xing528.com)
(5)结构阻尼为零。
以下分三种情况考虑失稳模型:
第一种情况:在桥梁横截面产生的顺风向两个连续旋涡的间距等于桥面宽度B的一半,如图5.8(a)。假设,扭转振动周期为T,振动周期开始时,一个旋涡位于在截面形心处下缘,形心处v=0,另一个旋涡正在截面上边缘迎风面形成,并未形成升力,则∑Fv=0。当t=T/8时,两个旋涡顺着截面漂移B/8,由于旋涡产生的升力和升力作用点的振动方向一致,则∑Fv>0。当t=T/4,两个旋涡顺着截面继续漂移B/8,升力作用点位于振幅幅值处,v=0,∑Fv=0。当t=3T/8,两个旋涡顺着截面漂移3B/8,升力作用点向平衡位置处振动,振动速度方向和升力相反,则∑Fv<0。到半个周期过后,两个旋涡都沿截面移动了B/2,迎风面处又开始产生新的旋涡,但产生于截面下缘。在随后的半个周期内,重复以上形式。经过分析,Fv在时间上的积分为0。
第二种情况:在桥梁横截面产生的顺风向两个连续旋涡的间距大于桥面宽度 B 的一半,如图 5.8(b)。按照第一种情况的分析方法,在一个振动周期内,∑Fv≥0,旋涡产生的升力不断对系统做功,系统通过增大振幅来吸收能量。
第三种情况对应于旋涡间距小于B/2,如图5.8(c)。一个周期内,∑Fv<0,扭转振幅不断减小。
塔科马大桥的破坏机理正是上述扭转模型的第二种情况。塔科马老桥的桥面很窄,旋涡间距和风速密切相关,风速的变化从而导致旋涡间距的变化。当风速满足一定的条件时,产生的旋涡的间距大于塔科马桥桥面宽度的一半,加劲梁不断地从气流中吸收能量,振幅不断地变大,形成发散的扭转,最终破坏。
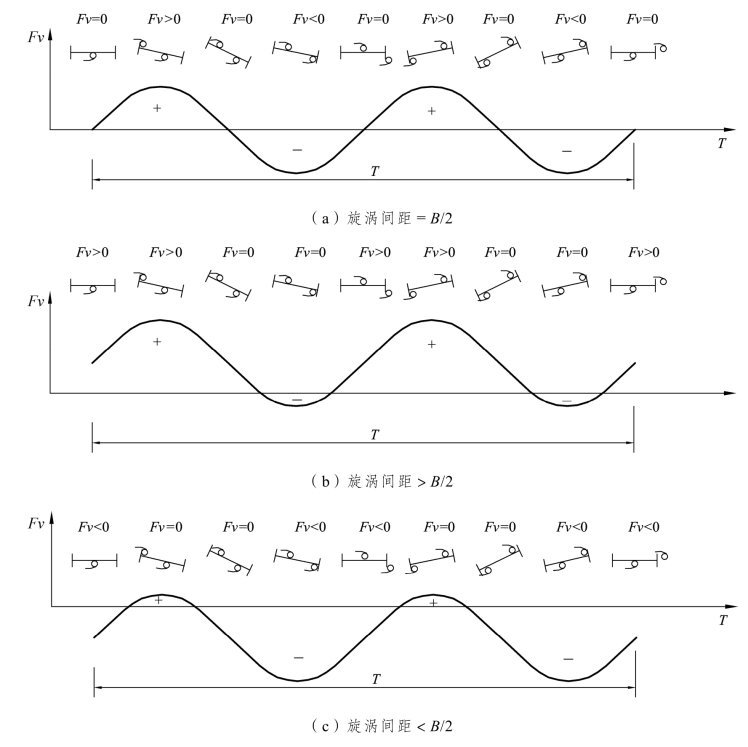
图5.8 不同连续漩涡间距下的结构振动
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




