世界著名钢桥失效事故分析：分析结果

1.静力分析

在静态垮塌模拟分析过程中，逐步增加活载系数Q计算相应的结构变形情况，图2.10所示为跨中处四点的竖向位移，当活载系数Q为12.5时，跨中挠度已达500 cm。恒载作用下四点处挠度均为20 cm。随着活载开始增加，各点的挠度基本相等。当Q增至4时，东侧节点挠度增加较快，当Q继续增加到10时，此时东北侧索和桁架似乎已到达承载能力极限，而东南侧结构相应松弛。此时桥梁绕纵轴可能发生了扭转，导致西侧结构挠度很小，如图2.11所示。

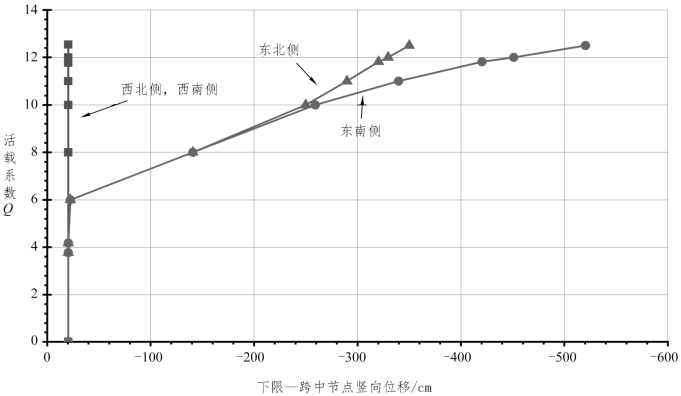
图2.10　跨中竖向位移下限分析

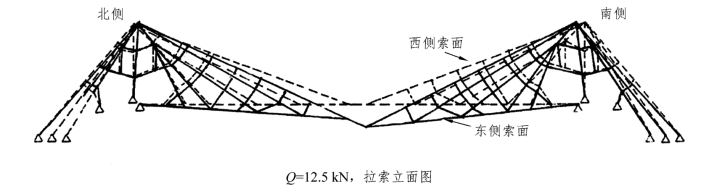
图2.11　Q=12.5 kN时的结构变形图

南桥塔顶部节点的水平位移如图2.12所示，结果与图2.10所示的桥面挠度几乎相等。恒载作用下的桥塔位移约9 cm。Q增至4时，东南桥塔顶部较快向跨中偏移，东南侧桥面挠度也随塔顶水平位移增加。当Q超过6时，东南侧背索拉长，东南侧塔柱向跨中倾斜，东南侧索和桁架单元向下挠曲，如图2.10中东南侧点所示。

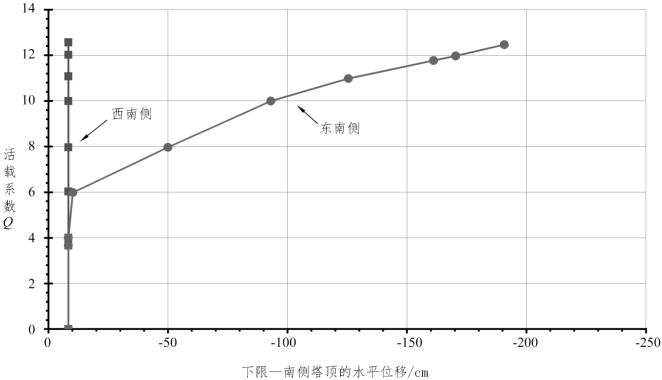
图2.12　塔顶纵向（水平）位移分析

由于背索断裂是垮塌的重要原因，图2.13分析了8根锻铁背索在活载作用下的内力变化情况（单元编号如图 2.7 所示）。恒载引起的背索内力非常大，施加活载后，结构体系发生内力重分布。图 2.14 分析了拉索应力的变化情况，东南侧拉索 213 应力达 255 MPa，拉索214和234应力达235 MPa，西南侧拉索113、114 和 134 应力较小，与东南侧拉索先断裂情况一致，此时活载系数Q=12.5 kN ，相当于255人，平均体重60 kg，与文献记载的282人相符[20，28]。与拉斯明·哈尔瓦[16]（Rasmine Halva）的计算结果（垮塌荷载约为285人，平均体重70 kg）很接近。(https://www.xing528.com)

图2.13　关键拉索内力

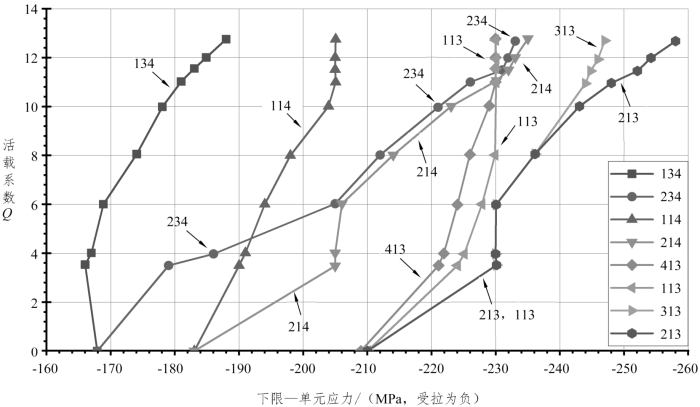
图2.14　关键拉索拉应力

2.动力分析

由于当时乐队的演奏节奏无法确定，参考一般情况，假定当时舞蹈的节奏为 1～3 s，对应的振动频率为 0.3～1.0 Hz。桥梁振动频率恰好在此范围内，就有可能对拉索应力产生重大影响。基于上述有限元分析模型，分析桥梁的固有频率。依据不同的恒活比分为两种工况，分析结果如下：

工况一：仅考虑恒载。假设结构是完全弹性的。拉索弹性模量E取图 2.8 所示应力-应变曲线第一阶段的弹性模量 193 258 MPa。计算得到前三阶固有频率分别为：1.19 Hz、1.21 Hz和1.75 Hz，第一阶振型为扭转。

工况二：恒载加 75% 活载。取桥梁倒塌时的282人，人均体重取60 kg，总活载166 kN，取75%活载，即124.5kN，分布如图2.11所示。活载作用下部分拉索应力超过了比例极限，此时E=154 362 MPa （应力-应变曲线前两段的平均值）。计算得到前三阶固有频率分别为0.98 Hz、1.05 Hz和1.50 Hz，第一阶振型为扭转。

工况一和二的分析结果表明，桥梁最小固有频率都很接近扰动频率，因此很有可能发生共振。如果发生共振，拉索应力将超过静载应力。当然现场不确定性因素较多，难以进行更详细的动力分析。