给定分布的随机变量抽样

由上述方法产生的伪随机数序列为[0，1]区间上的均匀随机数，实际问题中尚需变换为给定分布下的随机样本，以下讨论几种常见分布的变量抽样方法。

1.正态分布

产生正态变量随机数的方法，主要有哈斯汀《Hasting》有理逼近法、统计近似法、坐标变换法几种。其中坐标变换法产生随机数速度较快、精度较高，现介绍如下。

若已知γ1、γ2是[0，1]区间内的两个均匀随机数，则可用下列变换得到服从标准正态分布N[0，1]的两个随机数u1、u2

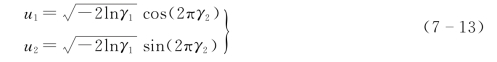
若x服从一般正态分布N（μx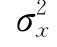，），则其随机数x1、x2通过u1、u2由下式计算求得

这种方法产生的随机数u1与u2或x1与x2成对出现，不仅相互独立且服从同一正态分布。

2.对数正态分布

对数正态分布变量随机数产生的方法是，先将均匀随机数变换为正态分布随机数，然后再转换为对数正态分布随机数。

设x为对数正态分布变量，则y＝ln x为正态分布，且其均值和标准差为

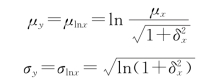
正态变量y的随机数可由式（7-13）、式（7-14）产生，则x的随机数为

3.极值Ⅰ型分布

极值Ⅰ型分布变量的随机数一般直接通过其概率分布函数得到。一般地，设变量x的分布函数为Fx（x），γi为[0，1]上均匀分布随机数，当Fx（x）＝γi时，相应于γi的随机数可由其逆函数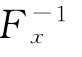（γi）求出，即

对于极值Ⅰ型分布，将

代入式（7-16）得到

其中　

将u、α代入式（7-17）得到

(www.xing528.com)

4.指数分布

设x服从指数分布，γi为[0，1]上均匀分布随机数，令

则指数分布随机数为

由于1—γi也是[0，1]上均匀分布随机数，故式（7-20）也可写为

【例7-2】 已知结构极限状态方程为Z＝g（R，S）＝R—S＝0，R服从正态分布，S服从极值Ⅰ型分布，统计参数为：μR＝100k N，σR＝20k N；μS＝80k N，σS＝24k N。试用蒙特卡罗法计算结构失效概率。

解：（1）产生[0，1]区间内均匀分布的随机数γi（见表7-2）。

（2）产生变量R，S的随机数Ri，Si。由式（7-18）及式（7-14）得到其计算公式为

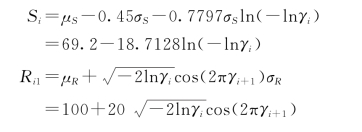
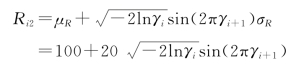
（3）把所得变量的随机数Si、Ri代入功能函数Z＝g（R，S）＝R—S＝0，求得Zi的值。

（4）重复（1）～（3）步，累积计算出现Zi≤0的次数n和总次数N。

（5）当计算次数足够大，如当为预估的失效概率），则计算结束，由pf＝给出计算结果。

本例前10次模拟计算所得的γi、Ri、Si、Zi及n值见表7-2，由表中结果可见，N＝10时n＝1，近似得到失效概率为

表7-2　蒙特卡罗法前10次计算结果

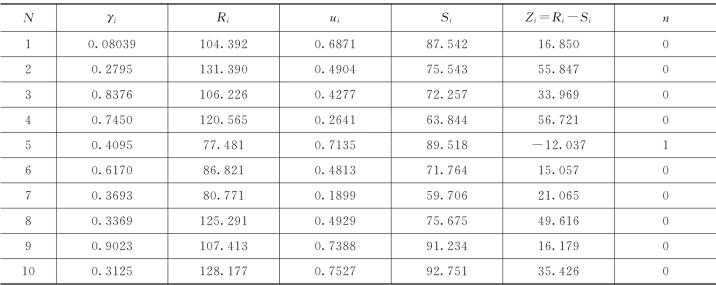
由于表7-2模拟次数太少，所得结果达不到精度要求。增加模拟计算的次数可提高计算的精度，表7-3给出了模拟1000次计算过程中的部分结果。由表中数据可见，算至500次以后，pf值趋于稳定，此时有pf≈0.2。若按此pf值估算最少模拟次数N，可得N＝500。由此也验证了pf与N的关系即式（7-4）。

表7-3　1000次模拟计算的部分结果

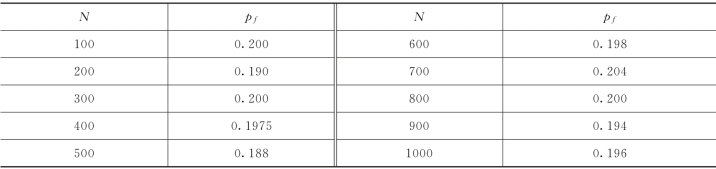
本例用验算点法求得β＝0.753，对应失效概率pf＝0.22，可见两者结果基本一致。

用蒙特卡罗法求结构的失效概率，计算量非常大，为减少抽样次数，提高抽样效益，有文献提出了改进的蒙特卡罗法，其中采用了改进的抽样方法，如条件抽样法，对偶抽样法等，提高pf的计算效率。有关内容请见有关文献[23]。