地震分项系数表达式设计

分项系数表达式将单一系数设计表达式中的安全系数分解为荷载分项系数和抗力分项系数，也有以变量均值表示的设计式和以变量标准值表示的设计式两种。

1.以均值或标准值表示的分项系数设计表达式

若结构的荷载效应由多个荷载引起，每个荷载效应都采用各自的分项系数，其分项系数设计表达式可写为如下形式

以均值表示时　

以标准值表示时　

式中　γ0si、γsi——荷载效应以均值表示或以标准值表示时的荷载效应系数，i＝1～n；

γ0R、γR——结构抗力分别以均值表示或标准值表示时的结构抗力分项系数。

一般情况下，结构的功能函数为

则分项系数设计表达式的一般形式为

基本变量以均值表示时

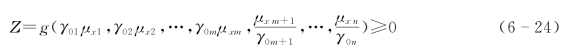
或写成　

基本变量以标准值表示时

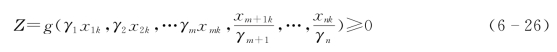
或写成　

一般分项系数采用大于或等于1的数值，因此荷载分项系数均以乘数出现，抗力分项系数均以除数出现[以上各式中，角标1～m为荷载变量编号；角标（m＋1）～n为抗力变量编号，s为任一个荷载变量号，γ为任一个抗力变量号]。

2.分项系数与可靠指标β及变量变异性的关系

由结构可靠度分析的验算点法，可知验算点坐标满足的极限状态方程为

或写成　

由式（5-76）得

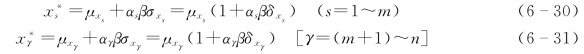
代入式（6-29）可得

比较式（6-32）与式（6-25）得到

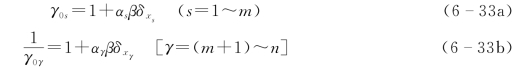
注意到变量均值与标准值的关系

将式（6-34a、b）代入式（6-32）有

比较式（6-35）与式（6-27）可得

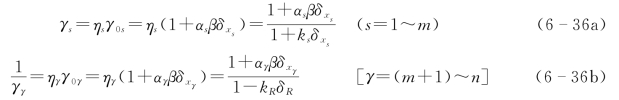
式（6-33）、式（6-36）即是变量分别以均值表示和以标准值表示时的分项系数（包括荷载分项系数和抗力分项系数）。各分项系数均与变量自身的变异系数和可靠指标β有关，当变量发生变异时，与之相应的分项系数随之变化。与单一系数设计表达式相比，分项系数设计表达式较容易适应设计条件的变化。在确定的分项系数下，可取得较好的结构可靠度一致性结果。因此，它也是各种规范设计准则采用的形式。

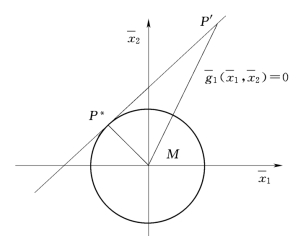
图6-2　二维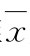空间

3.分项系数的不唯一性(www.xing528.com)

（1）功能函数Ζ中变量均为正态分布及Z为线性函数的情况。

首先将由正态变量xi构成的空间标准化为标准正态空间，在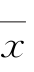空间内，结构极限状态方程为

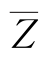＝0是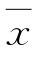空间内的一个线性曲面，如图6-2所示是二维情况。由可靠指标β的几何意义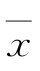，空间的坐标原点M到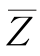＝0的距离就是可靠指标β（P*为验算点），由式（5-78）确定的αi是矢量（由M指向P*）的方向余弦，也是β矢量的方向余弦，因此αiβ是在 上的投影。

对于上任意点P＇，总可以选取一组α＇i（i＝1～n），使 在轴上的投影等于（注意α＇i并非的方向余弦，即），而进一步地，α＇iβ在MP*上的投影等于。

现将投影到上，由力学知识，合矢量 在上的投影等于其分矢量在上投影的代数和，即

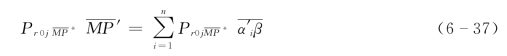
即是　

于是有　

由于P＇点在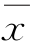空间中的坐标为，变换回到x空间得到P＇的坐标为

该点也在极限状态曲面，即有

因此可见，可在Ζ＝0上找到任意一点P＇，只要α＇i满足式（6-39），P＇点坐标与验算点坐标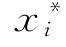具有相同的形式，并同样满足极限状态方程。

改写式（6-41）并代入P＇点坐标式（6-40）可得

g（…，x＇s，…，…，x＇γ，…）＝0

或　

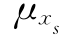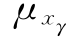用标准值表示及可得

比较式（6-42）与式（6-25）及式（6-43）与式（6-27），可得如下分项系数设计变量用均值表示时

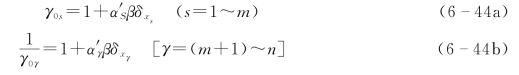
设计变量用标准值表示时

式（6-44）与式（6-45）即为不同于式（6-33）与式（6-36）的一组分项系数。由于P＇可在Ζ＝0上任意选取，因此就存在着无数组分项系数，只要满足式（6-39），都能满足可靠指标的要求。

（2）功能函数Ζ为非线性函数情况。

当Ζ＝g（x1，x2，…，xn）为非线性函数时，可用通过验算点的切平面来代替非线性的极限状态曲面，P＇点选择在切平面上，仍以与上述相同的方法可得出近似结果，只要非线性程度不很高，所得结果仍能满足设计要求。

（3）变量xi为非正态变量情况。

当功能函数Ζ＝g（x）中的变量xi为非正态分布时，P＇点坐标[见式（6-40）]中的统计参数需用当量正态变量的统计参数替代，即

此时式（6-42）可写为

或　

对比式（6-47）与式（6-25）得到

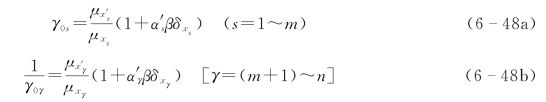
式（6-48）是当设计变量用均值表示时的分项系数。当设计变量用标准值表示时，其分项系数为：γS＝ηSγ0S，，即有

当设计需要时，可利用分项系数的不唯一性来求解。方法是按一定要求，先对n—1设计变量选定合适的α＇i及其分项系数，再按式（6-39）确定第n个αi及其分项系数。对于事先确定的分项系数，一般按变量变异性大小选定，变异性大的变量，分项系数相对大些。