地震荷载动力分析可靠度方法

由于结构体系的复杂性，精确计算其可靠度非常困难，工程中一般采用近似方法。这些近似方法大致可分为两类：区间估计法和点估法。区间估计法是利用概率论基本原理划定结构体系失效概率的上、下限；点估法则是采用适当近似处理，将复杂的多维积分转化为一般方法可以求解的问题。以下仅对串联体系与并联体系，简述基本计算方法。

1.结构体系可靠度的上下界（区间估计）

设结构体系由n个构件组成，其中各构件处于工作状态的事件为xi，处于失效状态的事件为， 各构件失效概率与可靠性概率分别为，结构体系的失效概率与可靠性概率分别为pf、ps。

（1）串联体系。串联体系可靠性的概率即体系内各构件处于工作状态的概率，即

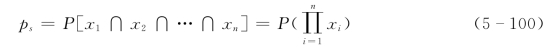
当x1，x2，…，xn完全独立时，式（5-100）变为

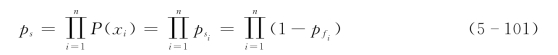
则串联体系的失效概率为

当x1，x2，…，xn完全（正）相关时，一旦某构件失效，由于相关性影响则整个体系失效。因而结构整体的失效概率取决于结构内工作状态最差者的失效概率，即有

此时串联体系的可靠性概率为

一般情况下，实际结构构件的工作状态既不完全独立，也不完全相关，而是在两者之间。因此一般串联体系的失效概率也介于上述两种极端情况的计算结果之间，即

（2）并联体系。并联体系的失效概率等于各构件均失效的概率，即

当构件工作状态完全独立时，有

当构件工作状态完全相关时，并联体系的失效概率等于体系内最后一个失效构件的失效概率，即

因此，一般情况下结构体系的失效概率在上述两种情况之间，即

由式（5-105）、式（5-109）可见：

（1）对于静定结构（串联体系），结构体系的可靠度总是小于或等于构件的可靠度。

（2）对于失效模式唯一的超静定结构（并联体系），结构体系的可靠度总是大于或等于构件的可靠度。

对于失效模式不唯一的超静定结构（串—并联体系），结构每一失效模式的可靠度总是大于或等于构件的可靠度（并联关系），而结构体系的可靠度总是小于或等于结构任一失效模式的可靠度（串联关系）。

上述为区间估计法的一般界限范围公式，它计算简单，但未考虑构件间和失效模式间的相关性，因此，一般求出的界限较宽，常用于结构体系可靠度的粗略估计。作为对该法的改进则有窄界限范围公式，请见有关文献[3]。

2.概率网络估算技术法

这是一种较为精确的点估近似方法，称PNET法（Probabilistic Network Evaluation Technique的简称）。其基本原理是，先将所有主要失效模式按彼此相关系数大小分成若干组，每组中选出一个失效概率最大的失效模式作为代表，再假定各代表失效模式相互独立，按下式估算结构体系的可靠度

或失效概率

式中　m——分组数。

PNET法计算步骤如下：

（1）列出主要失效模式及相应功能函数Zi，求出可靠指标βi，把βi由小至大排列，并将该序号作为代表失效模式排序的依据。

（2）选择定限相关系数ρ0（一般凭经验取为0.7或0.8，重要工程可取大些，偏安全），作为判别失效模式间相关程度的依据。

（3）寻找代表失效模式：取βi＝βmin者作为第一代表失效模式，并计算剩余失效模式与第一代表失效模式的相关系数ρj1（j＝2，3，…，n）。若ρj1≥ρ0，则认为第j失效模式与第一失效模式高级相关，可由第一代表失效模式所代替；若ρj1＜ρ0，则两者低级相关，不能被代替。在不能被第一代表失效模式代替的所有失效模式中找出βmin者作为第二代表失效模式，计算ρj2（j＝3，4，…，n），找出可以被第二代表失效模式代替的失效模式，再在不能被第二代表失效模式代替的所有失效模式中找出βmin者作为第三代表失效模式，如此继续下去，直至找出最后一个代表失效模式为止。

（4）用式（5-110）或式（5-111）计算结构体系的可靠度或失效概率。

该法考虑失效模式间的相关性，同时选代表失效模式进行计算，可大大减少工作量，是延性结构体系可靠性分析较为可行的方法。

当结构体系的功能函数Zi和Zj为非线性函数且用验算点法求β时，两个失效模式间的相关系数可采用如下公式计算

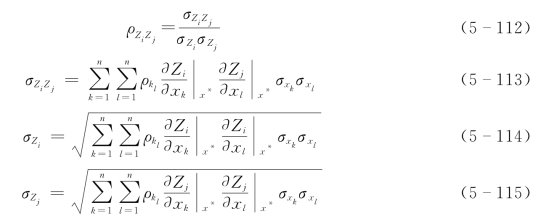
式中　——Zi与Zj的协方差；

——变量xk与xl间的相关系数；

——第i、第j失效模式的均方差。

图5-13　简支梁承受均布荷载

【例5-8】 已知如图5-13所示简支梁承受均布荷载q，截面1、2的功能函数为

Z1＝M1—8q

Z2＝M2—6q

M1、M2为截面1、2的弯曲抗力。M1、M2、q均服从正态分布且相互独立，统计参数分别为：＝600k N·m；＝60k N·m；＝460k N·m，＝46k N·m；μq＝50k N/m，σq＝5k N/m。求截面1、2功能函数Z1和Z2的相关系数。

解：（1）求。

由式（5-114）、式（5-115）得

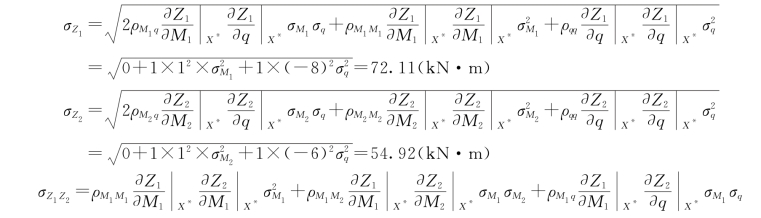
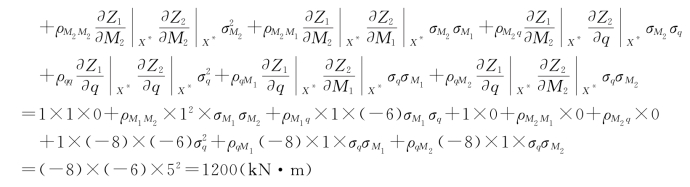
（2）求。

可见，即使基本变量相互独立，功能函数Z1与Z2仍具有一定相关性。

若M1与M2来自同一变量M，即M1＝M2＝M，且μM＝600k N·m，σM＝60k N·m，则有

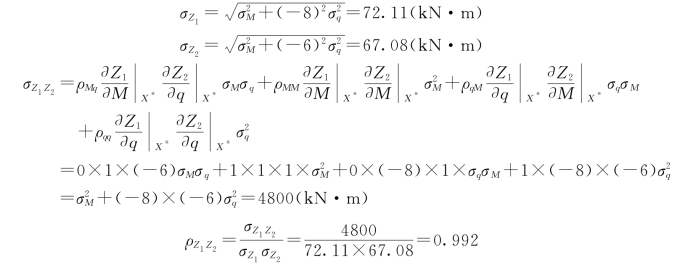
可见，与M1≠M2情况相比，相关系数ρZ1 Z2增大。一般地，结构体系失效模式中的公共变量愈多，失效模式间的相关性愈强。

【例5-9】 如图5-14所示悬臂梁，承受均布荷载q，其强度沿梁长均匀分布，梁任意截面的塑性抵抗力矩为M。已知q、M为正态分布且相互独立，μq＝60N/m，σq＝6N/m；μM＝5000N·m，σM＝500N·m，求该梁的可靠度。

图5-14　悬臂梁承受均布荷载

解：承受均布荷载q的悬臂梁，一般是在固端截面A首先形成塑性铰，其功能函数为

对应可靠指标为

失效概率　pf＝Φ（—β）＝Φ（—3.43）＝3.018×10—4

由于梁各截面强度具有随机性，不能排除任意x截面出现塑性铰的可能，因此本例属于体系可靠度问题。(www.xing528.com)

设x截面出现塑性铰，对应于该失效模式的功能函数为

利用式（5-112）可求得ZA与Zx的相关系数为

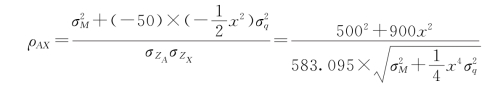
令x＝5，得　ρAX＝0.924

令x＝0，得　ρAX＝0.858

可见最小相关系数ρmin＝ρAX＞0.7（取ρ0＝0.7作为判别低级相关或高级相关的限定值），说明x为任意值时所有失效模式都与A截面出现塑性铰的失效模式高级相关，可由A截面失效模式代替。因此A截面出现塑性铰的失效模式是该梁唯一代表失效模式。体系失效概率为

p＝＝3.018×10—4

【例5-10】 某均布荷载作用的简支梁，可能发生弯曲失效E1或剪切失效E2，也可能发生弯剪组合失效E3。已知三种失效模式的失效概率为＝0.96×10—4，＝0.67×10—4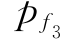，＝0.97×10—4。三种失效模式间的相关系数分别为ρ12＝0.0117，ρ13＝0.2754，ρ23＝0.044，试估算该梁的失效概率

解：由题意可知，该梁可用串联模型来计算，失效概率区间可用式（5-105）来估算，其中

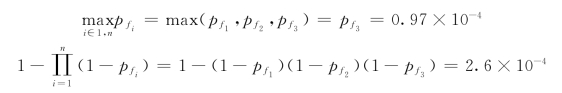
于是该简支梁失效概率的一般界限为

图5-15　钢丝索受力体系图

0.97×10—4≤pf≤2.6×10—4

可靠指标界限为　3.729≥β≥3.470

【例5-11】 设由3根钢丝索构成的受力体系（图5-15）承受荷载S，已知每根钢丝索的拉力R和荷载S均服从对数正态分布，其统计参数为：拉断力R：μR＝340k N，δR＝0.15；荷载S：μS＝540k N，δS＝0.25，求体系的失效概率，其中钢丝索按脆性元件计。

解：（1）题意分析：

1）由图5-15可见，该受力体系为超静定结构，任一失效模式为并联系统。且钢丝索为脆性构件，求体系失效概率需考虑元件失效顺序。

2）假定体系失效前，3根钢丝索的破坏是统计独立的，且在第1根拉断后，剩余钢丝索的破坏也是统计独立的。

3）令分别为每根钢丝索按顺序发生拉断事件Ⅰ、Ⅱ、Ⅲ的概率。由于独立性假定，出现一个体系失效模式（按顺序拉断）的体系失效概率为。此类失效模式共有6种，即：1，2，3；1，3，2；2，3，1；2，1，3；3，1，2；3，2，1，各失效模式间为串联系统。

4）由于各丝索拉断力R服从同一分布，有相同统计参数值。故按顺序拉断事件不是互斥的，即也可能2根钢丝索同时拉断或3根钢丝索同时拉断而导致体系失效。2根钢丝索拉断时也可能2根钢丝先发生同时拉断剩余1根钢丝索后拉断，或1根钢丝索先拉断后剩余2根钢丝索再同时拉断，前者对应的失效模式有3种：表示同时拉断的钢丝索），每一种失效模式的体系失效概率为（同时先断的2根钢丝索，其受力状态等同于按顺序拉断时第Ⅰ顺序被拉断的钢丝索，故其失效概率均为。后拉断的钢丝索受力状态等同于按顺序拉断时第Ⅲ顺序被拉断的钢丝索，失效概率为）。后者对应的失效模式亦有3种：，每一种失效模式的体系失效概率为（先拉断的钢丝索受力状态等同于按顺序拉断时第Ⅰ顺序被拉断的钢丝索，失效概率为，同时后拉断的2根钢丝索，其受力状态等同于按顺序拉断时第Ⅱ顺序被拉断的钢丝索，故其失效概率为）。3根钢丝索同时拉断的失效模式只有1种，体系失效概率为（此时每一钢丝索的受力状态等同于按顺序拉断时第Ⅰ顺序被拉断的钢丝索，失效概率均为）。

（2）体系失效概率。设钢丝索按顺序拉断导致体系失效的事件为Xi，2根钢丝索同时拉断导致体系失效的事件为Xi Xj，3根钢丝索同时拉断导致体系失效的事件为Xi Xj Xk，一般地，若为n根钢丝索且每一钢丝索拉断不互斥时，由概率论知，体系失效概率为

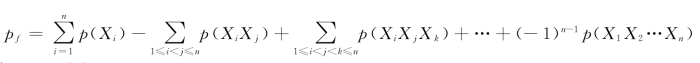
当n＝3时有

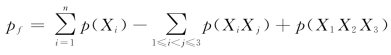
对于本例即有

（3）及pf计算。

第Ⅰ钢丝索拉断时的极限状态方程为

第Ⅱ钢丝索拉断时的极限状态方程为

第Ⅲ钢丝索拉断时的极限状态方程为

由式（5-30）可求得Z1、Z2、Z3的可靠指标βi与失效概率为

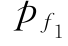＝Ф（—β1）＝Ф（—2.181）＝0.0146

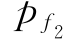＝Ф（—β2）＝Ф（—0.791）＝0.2145

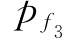＝Ф（—β3）＝Ф（1.587）＝0.9437

结构体系的失效概率为

pf＝6×0.0146×0.2145×0.9437—3×（0.01462×0.9437＋0.0146×0.21452）＋0.01463＝0.0151

比较pf与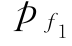可知，pf比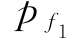仅相差0.0005。因而，对于由脆性元件构成的超静定程度不高的并联体系，可按串联模型考虑。一般当第一个元件失效，则可近似认为整个结构体系失效。

图5-16　静定桁架承受集中荷载

【例5-12】 求图5-16所示静定桁架的可靠度。已知节点荷载P及结构内7根杆件的拉、压抗力R1～R7均为正态分布，且相互独立，其统计参数为μp＝5k N，σp＝0.5k N；。

解：（1）失效模式及相应功能函数。

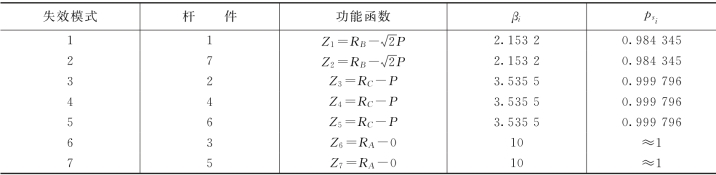
本桁架为静定结构，故为串联体系，其中任一杆件失效则体系失效，共有7个失效模式。由于杆件数目不多，7个失效模式均视作主要失效模式。由静定平衡可得各杆件的功能函数，见表5-6。

表5-6　各失效模式的Zi、βi及值

（2）求各失效模式的可靠指标βi及可靠度。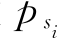

由式（5-23）可得各失效模式的可靠指标βi。例如β1及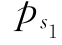计算如下

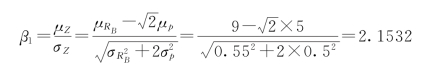
则功能函数Z1的可靠度为

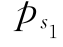＝Ф（＋β1）＝Ф（＋2.1532）＝0.984345

同理求得其余杆件的βi及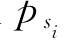值，见表5-6。

（3）寻找代表失效模式。

按照PNET法，将各失效模式按β值从小至大的顺序排列，见表5-6第4列。并按式（5-112）求各失效模式的相关系数ρij。如ρ13计算如下

同理可求得其余失效模式的相关系数ρij，见表5-7。

表5-7　各失效模式的相关系数ρij值

取定限相关系数ρ0＝0.7，由表5-7可知：

ρ12＝1.0＞ρ0，故失效模式2可由失效模式1代替；

ρ34＝ρ35＝1.0＞ρ0，故失效模式4、5可由失效模式3代替；

ρ67＝1.0＞ρ0，故失效模式7可由失效模式6代替。

因此找出代表失效模式为1、3、6。

（4）求结构体系的可靠度ps。

由式（5-110）可得该桁架体系的可靠度为

ps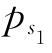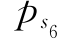＝＝0.984345×0.999796×1.0＝0.984145