超静定结构的失效模式和相关性

1.结构构件的失效性质

对一个结构体系而言，其组成构件的失效性质决定着整个体系的失效形态和体系的可靠度。对于构成整个结构体系的诸构件（包含连接件），按其材料和失效后的形态不同，可分为脆性和延性两类。

若构件在失效后不再起作用，即一旦失效则完全丧失功能的构件，称为脆性构件。例如脆性材料制成的拉杆，钢筋混凝土受压柱等，一旦破坏即失去承载力。

若构件在失效之后仍能保持其荷载水平，即失效后仍能维持原有功能的构件，称为延性构件。例如由具有明显屈服极限的钢材制成的受拉构件或受弯构件，受力达到屈服承载力时仍能保持该承载力而继续变形。

2.结构体系的失效模型

按结构体系失效与构件失效之间的逻辑关系，结构体系失效可分为串联、并联、串-并联等几种形式。

（1）串联模型。若结构中任一构件失效则整个结构失效，这种结构体系称为串联体系，可用串联模型来表示。

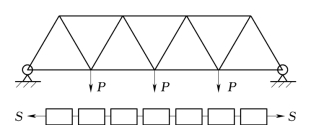
图5-9　静定桁架与串联模型

所有静定结构均可视为串联体系。如图5-9所示，静定桁架即为一典型串联体系。其中每一杆件可视为串联模型中的一个元件，只要其中一个元件失效，则整个体系失效。对于静定结构，其构件的失效性质（脆性或延性）对结构体系的可靠度不产生影响。

（2）并联模型。若在结构中，总有冗余构件可能承受重新分配的外部荷载，使得一个构件或几个构件失效后，剩余的构件与失效的延性构件仍能维持原结构体系的功能，仅当所有构件失效整个结构体系才失效，这类结构体系称为并联体系，可用并联模型来表示。

超静定结构可视为并联体系。如图5-10所示的多跨排架结构，其中假定只有柱子可能失效，每一柱子可视为并联模型的一个元件，只有当所有柱子均失效才导致整个结构体系失效。又如图5-11所示两端固定的钢质梁，仅当梁两端和跨中截面均出现塑性铰（塑性铰截面当作一个元件），整个梁才失效。(www.xing528.com)

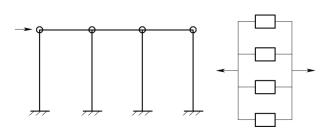
图5-10　排架结构与并联模型

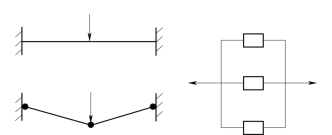
图5-11　超静定梁与并联模型

在并联体系中，构件的失效性质影响结构体系的可靠度及其计算模型。脆性元件失效后将逐个从体系中退出工作，因此结构体系可靠度计算时，需考虑构件的失效顺序。而延性构件失效后仍能在体系中维持原有功能，因此只考虑体系最终失效形态。

（3）串—并联模型。对于由延性构件组成的超静定结构，往往有多种失效模式，其中每一种失效模式都是一个并联体系，这些并联体系又组成串联体系，因而形成串—并联体系，这种体系可用串—并联模型来表示。例如，如图5-12所示的单层钢质框架，其中假定受载后以最终形成塑性铰机构而失效。由力学分析知，其失效模式可能有三种，任一种失效模式实际出现，则结构体系失效，属于串联体系。而在每一种失效模式中，只有全部元件（塑性铰截面）均失效，结构体系才失效，属于并联体系，因此可用串—并联体系模拟。

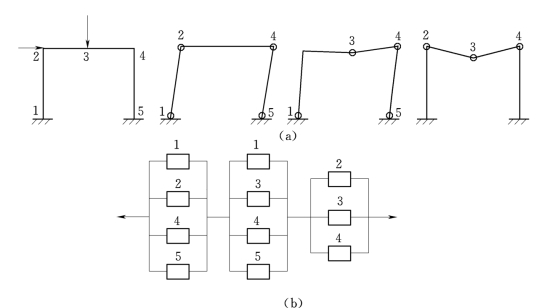
图5-12　超静定结构与串—并联模型

需指出，对于由脆性构件组成的超静定结构，若超静定程度不高，当其中一个构件失效而退出工作后，随后的其他构件失效概率大大增加，几乎不影响结构体系的可靠度，这类结构的并联子系统可简化为一个元件，因而可按串联模型处理（见[例5-8]）。

实际工程中大多数超静定结构可模拟为串—并联体系，也有一些可模拟为并—串联体系（若干串联模式的并联体系），但相对较少，有关研究也不多见。

对于复杂工程结构，失效模式往往很多，而对结构体系可靠度影响较大的是那些出现可能性较大的失效模式，称主要失效模式或主要失效机构。确定主要失效模式常是体系可靠度分析的关键，其确定方法有荷载增量法、假定塑性铰位置的失效机构法、逐段线性弹塑性矩阵分析法等，这方面内容请见文献[20]。

（4）构件间和失效形态间的相关性。结构体系可靠度分析中，可能出现至少两种形式的相关性，即单个构件间的相关性和失效模式间的相关性。这是由于在同一结构中，各构件的荷载效应来源于同一荷载，使不同构件的荷载效应之间存在相关性；结构体系内，部分或全部构件可能由同一材料制成，因而使构件的抗力之间也存在相关性，即构成了构件间的相关性。超静定结构不同失效模式常包含相同的失效构件（图5-12），因此构成了失效模式间的相关性。上述相关性常由它们相应的功能函数间的相关系数来反映。