地震荷载动力分析与结构可靠度设计原理中的验算点法

当结构功能函数为非线性函数时，先将其在验算点处线性展开，见式（5-68），并对功能函数中的非正态变量在验算点处当量正态化，用当量正态变量x＇i代替原非正态分布变量xi，其均值、标准差由式（5-82）、式（5-85）求出。

经过对基本变量当量正态化和对功能函数线性化，结构功能函数g（x1，x2，…，xn）可表达为

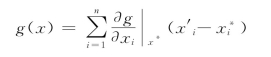
式中　x＇i——当量正态化变量，若xi为正态变量时，x＇i＝xi。

分析表明，非正态变量的当量正态化并不改变随机变量间的线性相关性，即有。通过当量正态化变换，将非正态变量的可靠度分析转化为正态变量的可靠度分析后，则可用类同于5.3.2的方法推得如下计算公式

功能函数均值　

功能函数标准差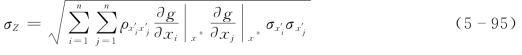　

β的方向余弦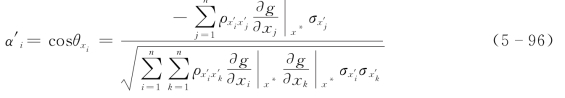　

验算点坐标　

式中，当变量为正态变量时，x＇i＝xi。当x1，x2，…，xn相互独立时，式（5-95）简化为

式（5-96）简化为式（5-78）。

由于验算点在极限状态曲面上，故满足

式（5-96）、式（5-97）、式（5-99）则为考虑变量间相关性影响时，迭代求解可靠指标β的验算点法方程组，其计算步骤为：

（1）给定验算点初值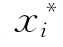，一般取为变量的均值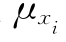（相当于设β初值为0的情况）。

（2）对非正态变量进行当量正态变换，求出当量正态变量的均值和标准差。

（3）应用式（5-96）求β的方向余弦α＇i。

（4）应用式（5-97）计算验算点坐标的新值（其中β为未知量）。

（5）由式（5-99）求解β的新值。

（6）以β、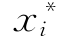的新值代替上一次迭代的初值重复（2）～（5）步，直至前后两次β值充分接近为止。

当结构功能函数复杂时也可采用如下步骤：

（1）给定β、xi的初值，即β0＝0，。

（2）当量正态变换，对非正态变量xi求出其当量正态变量的统计参数。

（3）由式（5-94）与式（5-95）求解。

（4）由式（5-96）求β的方向余弦α＇i。

（5）由式（5-97）求验算点的新值[式中β已由（3）步求出]。

（6）将（5）步求出的代入式（5-99），验算是否满足。(www.xing528.com)

（7）若不满足g（x*）＝0，则以新值代替（1）步中的初值，重复（2）～（6）步，直至满足要求为止。

【例5-7】 已知结构极限状态方程为g（x）＝x1x2—130＝0，其中x1和x2的均值和变异系数分别为＝38.0，＝0.10；μx2＝7.0，＝0.15。且知x1为对数正态分布，x2为正态分布，x1与x2相关系数为ρ12＝0.5，求结构的可靠指标β。

解：迭代一：

（1）设验算点初值。

（2）对变量x1进行当量正态变换，求变换后的均值与标准差。

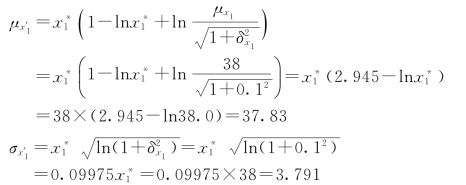
（3）求灵敏度系数α＇i。

对于正态分布变量x2，标准差为

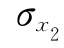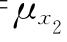
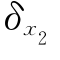＝＝7×0.15＝1.05

由式（5-96）可得

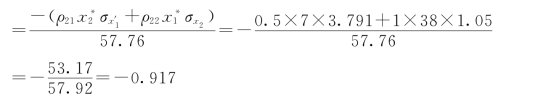
（4）求验算点新值。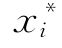

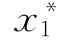＝＝37.83—0.803×3.791β＝37.83—3.04β

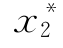＝＝7—0.917×1.05β＝7—0.96β

（5）求可靠指标β。

将代入x1x2—130＝0可得

（37.83—3.04β）×（7—0.96β）—130＝0

解出　β1＝2.72

由于β1≠β0，需进行第二次迭代，以验算点新值

＝37.83—3.04β＝37.83—3.04×2.72＝29.56

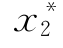＝7—0.96β＝7—0.96×2.72＝4.39

代替迭代一中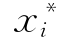初值，重复（2）～（5）步计算。依此类推，直至前后两次求出的β值十分接近为止。

本例经4次迭代得β＝2.778。为便于比较，表5-5给出了两种情况：①x1、x2均服从正态分布；②x1对数正态分布、x2正态分布，相关系数ρ12＝±0.9、±0.5、±0.2、0.0时β的计算结果。

表5-5　不同ρ值时β的计算结果

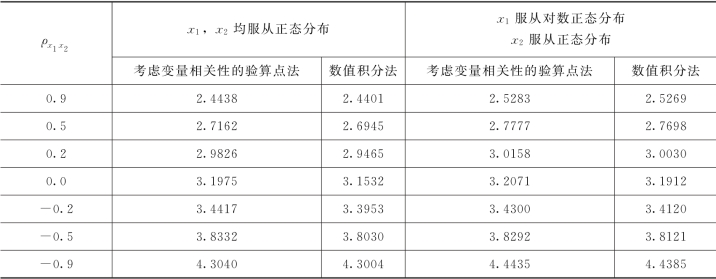
为了比较，表5-5中还给出了数值积分法计算结果（精确值）。由表5.5中数据可见，计入变量相关性影响的验算法计算结果有较好的精度。