中心点法的地震荷载动力分析与可靠度设计

设结构功能函数为

Z＝g（x1，x2，…，xn）

将Z在基本变量的均值点处展开为泰勒级数并取至线性项，有

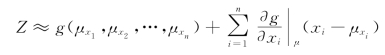
考虑变量间相关性时，Z的均值和标准差为

μZ＝g（，，…，）

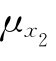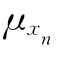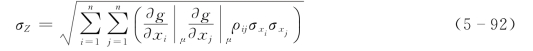
则结构可靠指标为

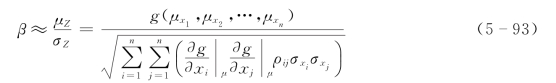
式中　ρij——变量xi、xj间的相关系数，当i≠j时|ρij|≤1，当i＝j时|ρij|＝1。

当所有基本变量相互独立时，即i≠j时ρij＝0，则式（5-93）成为式（5-37）。

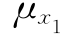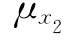【例5-5】 已知结构功能函数g（x）＝x1—x2。x1、x2为相关正态随机变量，统计参数为：＝2.0，＝0.24；＝1.0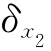，＝0.15。x1与x2相关系数ρ21＝ρ12＝ρ，求ρ值分别为0.9、0.45、0.1、0.0、—0.1、—0.45、—0.9时的可靠指标β。

解：由式（5-93）得

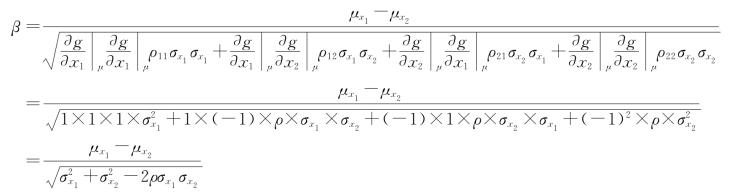
其中　＝2×0.24＝0.48；＝1×0.15＝0.15(www.xing528.com)

当ρ＝0.9时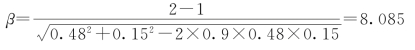　

当ρ＝0.0时　

当ρ＝—0.9时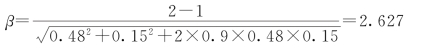　

可见ρ值不同时β值不同，其他ρ值时的可靠指标β计算结果见表5-3。

表5-3　不同ρ值时的β值

【例5-6】 [例5-5]中条件不变，仅将功能函数变为如下非线性函数

g（x）＝4＋—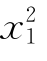

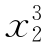
求不同ρ值的可靠指标β。

解：由式（5-93）可得

由上式求出ρ＝±0.9、±0.45、±0.1及0时的β值，见表5-4。

表5-4　不同ρ值时的β值

由上述例题计算结果可见，结构功能函数中随机变量间的相关性对结构可靠指标有一定影响。