中心点法计算梁截面功能函数及失效概率

1.结构功能函数为线性情况

设结构功能函数有如下形式

式中　a0、ai（i＝1～n）——已知常数；

xi——相互独立的随机变量。

由式（4-2）、式（4-3）可求得Z的均值和标准差为

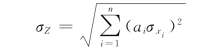
式中　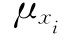、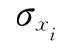——xi的均值和标准差。

根据中心极限定理，当n充分大时，不论xi（i＝1～n）为何种分布，只要彼此独立，则Z趋近于正态分布。因此当n较大时，可应用式（5-19）近似计算可靠指标，即

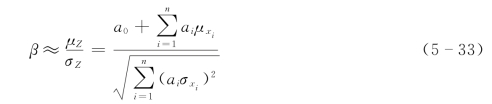
结构失效概率按式（5-21）计算。

【例5-2】 如图5-3所示简支梁。P为跨中集中力、q为均布荷载、L为跨度。该梁跨中截面承载力的功能函数为

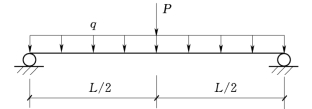
图5-3　简支梁受力图

已知变量统计参数为：μp＝10k N，δp＝0.1；μq＝2k N/m，δq＝0.15；μM＝18k N·m，δM＝0.05；L为常数，L＝4m。试用中心点法计算可靠指标β。

解：（1）先求基本变量的标准差。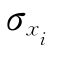

σp＝μpδp＝10×0.1＝1.0（kN）

σq＝μqδq＝2×0.15＝0.3（k N/m）

σm＝μmδm＝18×0.05＝0.9（k N·m）

（2）求功能函数的均值μZ[对Z应用式（4-2）]。

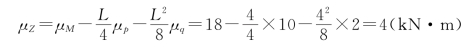
（3）求功能函数的标准差σZ[对Z应用式（4-3）]。

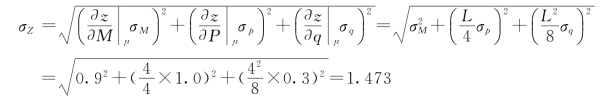
（4）求可靠指标β。

于是结构失效概率为

pf＝Ф（—β）＝Ф（—2.715）＝3.314×10—3

2.结构功能函数为非线性函数情况

大多情况下结构功能函数为非线性函数，设

式中　x1，x2，…，xn——n个相互独立的随机变量，其均值、标准差为、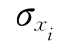（i＝1～n）。

将功能函数在随机变量的均值点（中心点）处展开为泰勒级数并取至线性项，即

式中中的下标“μ”表示在变量均值点（）处赋值。

对式（5-35）应用式（4-2）及式（4-3）可得功能函数的均值和标准差近似为

由中心极限定理知，当n充分大时，Z近似为正态分布，因此结构可靠指标为

【例5-3】 已知简支梁受力图同[例5-2]，其中p、q统计参数不变，即μp＝10k N，δp＝0.1；μq＝2k N/m，δq＝0.15。其他变量及统计参数为：梁跨中截面抵抗弯矩M＝ωpf，其中截面抵抗矩ωp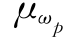：＝0.9×10—4 m3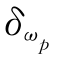，＝0.04；材料强度f：μf＝20×104 k N/m2，δf＝0.05；梁跨度L：μL＝4 m，δL＝0.05。梁跨中截面抗弯承载力功能函数为

采用中心点法计算可常指标β及失效概率pf。

解：（1）求功能函数均值μZ。

对功能函数Z应用式（4-2）得

（2）求变量标准差。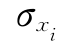

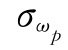＝＝0.9×0.04＝0.036×10—4（m3）

σf＝μfδf＝20×0.05＝1×104（k N/m2）

σL＝μLδL＝4×0.05＝0.2（m）

σp＝1.0k N

σq＝0.3k N/m

（3）求功能函数标准差σZ。

对功能函数Z应用式（4-3）得到

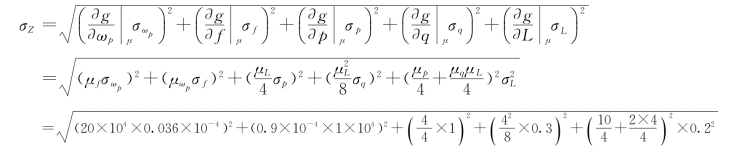
（4）求可靠指标β及失效概率pf。

则　pf＝Ф（—β）＝Ф（—2.139）＝1.622×10—2

3.可靠指标β的几何意义

由前述知，在结构功能函数Z的标准化概率密度曲线上，|—β|是失效边界至原点（均值点）的距离。现进一步讨论，在功能函数Z所涉及的基本变量x1，x2，…，xn所构成的空间中，β与极限状态方程Z＝g（x1，x2，…，xn）＝0（或称失效曲面）的关系，即β的几何意义。

（1）功能函数为线性的情况。

对应于线性功能函数式（5-31），结构的极限状态方程为

设式中xi（i＝1～n）为独立正态分布的随机变量，标准化变换如下：

令　

则　

将式（5-40）代入式（5-38）可得

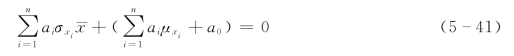
将式（5-41）两边同除以—， 并对常数项取模，则

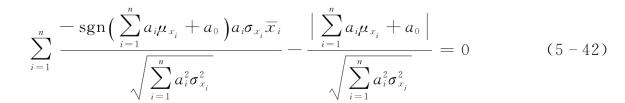(www.xing528.com)

式中　sgn（·）——符号函数，其函数值与（ ）中变量的±号有关，当y＞0时，

sgn（y）＝1；y＜0时，sgn（y）＝—1；y＝0时，sgn（y）＝0。

令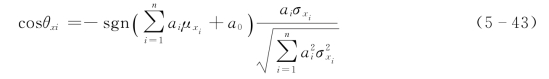　

则式（5-42）变为

由式（5-43）显见

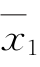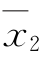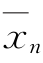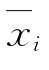由数学知识可知，式（5-45）代表，，…，空间中一线性平面，该平面至坐标原点的最短距离为d，该平面法向矢量与轴夹角的方向余弦为，该平面单位法向矢量为

注意到，d（原点至平面的最短距离）与平面法向矢量方向一致，所以n的方向余弦也是d的方向余弦。

比较式（5-44）与式（5-33）知

由此可得结论Ⅰ：当x1，x2，…，xn为独立正态随机变量时，且极限状态方程是x1，x2，…，xn空间中一线性曲面，则在其标准化空间中，该极限状态曲面至原点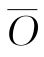的距离即为可靠指标的绝对值。

图5-4表示了基本随机变量为二维情况下，线性极限状态曲面时β的几何意义。

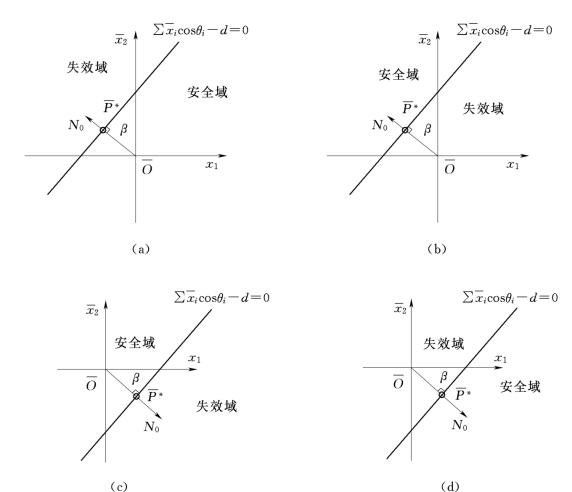
图5-4　二维情况线性极限状态曲面时β的几何意义

（a）β＞0；（b）β＜0；（c）β＞0；（d）β＜0

（2）功能函数为非线性函数的情况。

当Z＝g（x）为非线性函数时，其极限状态方程式（5-5）

g（x）＝g（x1，x2，…，xn）＝0

为一非线性曲面。此时若在g（x）＝0上取一点x0，过x0点作g（x）＝0的切平面[即将g（x）＝0在x0点展开为泰氏级数取至线性项]R（x）＝0，即

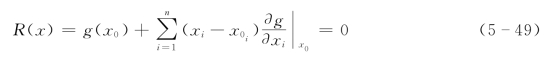
式中　——独立正态随机向量。

同样引入标准化变量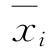，将式（5-40）代入式（5-49）得

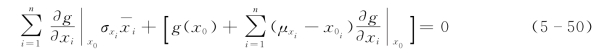
如将x0点取为均值点μ，即

则式（5-50）成为

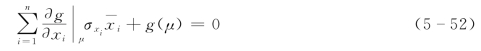
两边同时除以，则式（5-52）可转化为空间中的标准化线性方程，即

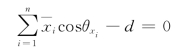
其中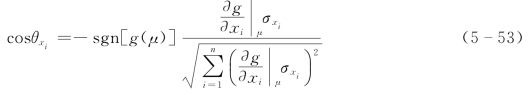　

比较式（5-54）与式（5-37），同样可得

d＝|β|

由此得出结论Ⅱ：当结构功__能函数为独立正态随机向量x的非线性函数时，在标准化空间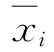 （i＝1～n）中，原点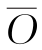到过极限状态非线性曲面上某点（常取为均值点）切平面的距离近似等于可靠指标的绝对值。

图5-5表示了当随机向量为二维情况，非线性极限状态曲面时β的几何意义。

由图5-4及图5-5可见，β＞0时，原点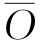位于可靠域内；β＜0时原点位于失效域内。

（3）误差分析。

根据β的几何关系，结构可靠指标计算可转化为标准正态化空间中失效平面（Z＝0为线性函数）到原点的距离或失效曲面（Z＝0为非线性函数）上过均值点的切平面到原点的距离来计算。对于后者，由于真实失效曲面由切平面近似代替而存在误差。现对失效面为单曲面（曲面不改变弯曲方向，即不改变＋、—符号）情况讨论如下：

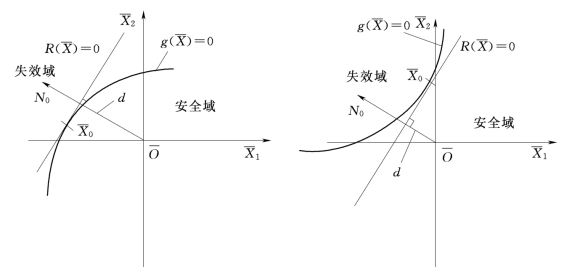
图5-5　二维情况非线性极性状态曲面时β的几何意义（β＞0）

1）失效面为下凹曲面，如图5-6（a）所示。此时极限状态方程线性化带来的结构失效概率误差为

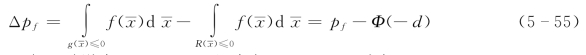
为了减小|Δpf|，需增大Ф（—d），即减小d。d＝dmin时有

几何上可以证明

式中　Dmin——原点到＝0的最短距离。

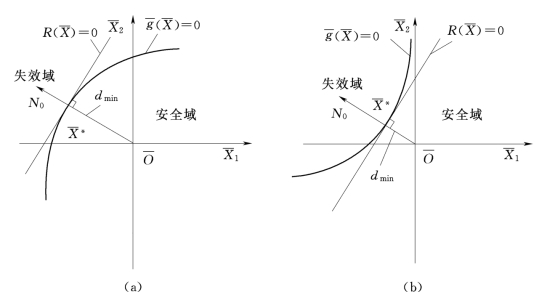
图5-6　标准化空间中原点到极限状态曲面的最短距离

2）失效面＝0为上凹曲面，如图5-6（b）所示。此时

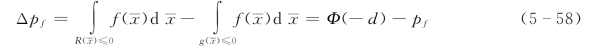
为了减小|Δpf|，需减小Ф（—d），即增大d，d＝dmax时有

几何上亦可证明

从式（5-56）、式（5-57）、式（5-59）、式（5-60）知，不论失效面为上凹或下凹，均有d＝Dmin时，从而可得

近似计算时可取

由此得出结论Ⅲ：当x＝[x1，x2，…，xn]T为独立正态随机向量，且在x的标准正态化空间中，极限状态曲面为单曲面时，用原点到极限状态曲面的最短距离Dmin代替可靠指标β求pf产生的误差最小。

4.中心点法的优缺点

中心点法最大优点是计算简便，不需进行过多复杂的计算，但也存在以下明显不足：

（1）不考虑基本随机变量的分布概型。该法建立在正态分布随机变量的基础上，实际变量为非正态分布时均按正态或对数正态处理，计算结果显然存在误差。

（2）将非线性函数在随机变量的均值点处展开并非合理，因为随机变量的均值不在极限状态曲面上，由于设计时出于结构可靠性的要求，均值点一般离开极限状态曲面有相当的距离，因而在均值点处展开的线性极限状态曲面可能会较大程度地偏离原来的极限状态曲面，由此造成的误差不可避免。

（3）力学含义相同、数学表达式不同的极限状态方程，由中心点法求得的可靠指标可能不同。例如，直径为d，屈服强度为fy，受轴向拉力为p的钢杆，极限状态方程可有两种

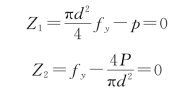
当d、fy、p统计参数分别为：μd＝14mm，σd＝0.7mm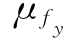；＝355MPa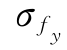，＝26.8MPa；μp＝25k N，σp＝6.25k N时，可求得β1≠β2（β1＝2.92、β2＝3.37）。可见对同一力学问题，采用不同形式的极限状态方程，所得结构可靠指标β不同，且相差较大，这是中心点法的一个严重不足之处。