地震荷载分析工程结构可靠度设计

设在结构功能函数Z＝R—S中，R、S是互相独立的正态随机变量，其均值和标准差分别为μR、μS和σR、σS。由概率论知，Z也为正态随机变量，均值μZ和标准差σZ分别为

则结构失效概率为

引入标准化变量y（μy＝0，σy＝1），即令

此时，，当Z从—∞→0时，y从，式（5-16）成为

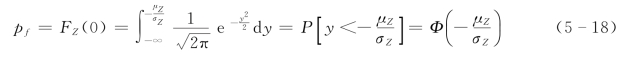
式中　Ф（·）——标准正态分布函数值。

令　

或　

式（5-18）成为

或　

比较式（5-20）与图5-2（a）可知，在功能函数Z的概率密度曲线上，乘积βσZ等于失效边界（Z＝0）至均值点（Z＝μZ）的距离。对于一定的结构，若β值愈大，则失效边界距离均值点愈远，图中阴影响部分的面积（即pf）愈小，反之则大。

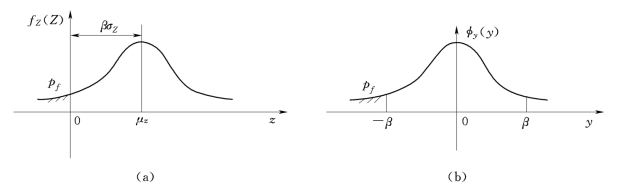
图5-2　pf与β的关系

由图5-2（b）及式（5-22）可知，在Z的标准正态化变量y的概率密度曲线上，y＝—β是失效边界，也是标准正态概率分布函数Ф（y）上对应于结构失效概率pf的分位值，β与pf之间存在一一对应关系；β小时pf大，β大时pf就小。因此β与pf一样，可以作为衡量结构可靠性的一个指标，称为结构可靠指标。在结构可靠度分析与设计中，β具有十分重要的意义。目前各国设计规范普遍采用了结构可靠指标β的概念。(www.xing528.com)

将式（5-14）、式（5-15）代入式（5-19），可得R、S均为正态随机变量时β的表达式，即

若R、S均为对数正态分布，结构功能函数可表示为如下形式

此时Z服从正态分布，其均值和标准差为

式中　μlnR、μlnS——ln R、ln S的均值；

σlnR、σlnS——ln R、ln S的标准差。

由概率论知，对于对数正态变量X，其对数ln X的统计参数与X本身统计参数间的关系为

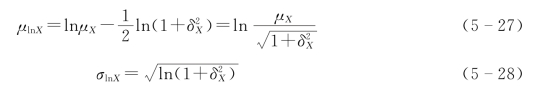
式中　μX、δX——X的均值和变异系数。

将式（5-27）、式（5-28）分别应用于式（5-25）、式（5-26）后再代入式（5-19），可得

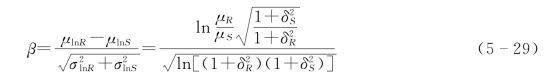
式（5-29）即为R、S均为对数正态分布时结构的可靠指标。特殊地，当δR、δS均小于0.3时，式（5-29）可进一步简化为

结构失效概率pf仍可由式（5-21）求出。表5-1给出了可靠指标β与失效概率pf的对应关系。

表5-1　β与pf的关系