地震荷载动力分析及结构可靠度设计

一般地，结构构件可能由几种材料组成，且当同时考虑结构构件的材料性能、几何参数、计算模式不定性影响时，抗力可用随机变量R表达为

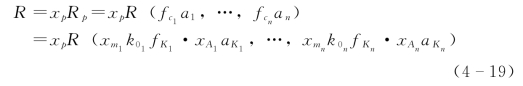
式中　Rp——由计算公式确定的结构构件抗力，R（·）是Rp的函数；

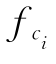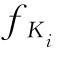、——结构构件中第i种材料性能的实际值和标准值；

ai、aKi——与第i种材料相应的结构构件几何参数的实际值和标准值；

——结构构件中第i种材料性能不定性变量；

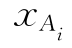——与第i种材料相应的结构构件几何参数不定性变量。

R的统计参数表达式有以下两种情况：

（1）特殊地，构件为轴心拉压且由单一材料组成时，式（4-19）可简化为

对式（4-20）应用式（4-2）～式（4-4）可得到R的统计参数

均值　

令　

式中　RK——抗力标准值，由材料性能标准值和几何参数标准值（设计值）计算得到；

ηR——结构构件抗力的均值与标准值之比。

抗力R的变异系数为

（2）一般地，由多种材料组成的一般受力构件，抗力表达式采用式（4-19）的如下形式

对式（4-25）应用式（4-2）～式（4-4）可得其统计参数为

均值　

变异系数　

R的均值与标准值之比　

式中，RK可由在Rp的表达式中赋予变量（材料性能、几何参数）标准值求出。

各种常见结构构件抗力R的统计参数ηR、δR值见表4-5。计算基本方法见[例4-4]及[例4-5]。

表4-5　各种结构构件抗力R的统计参数

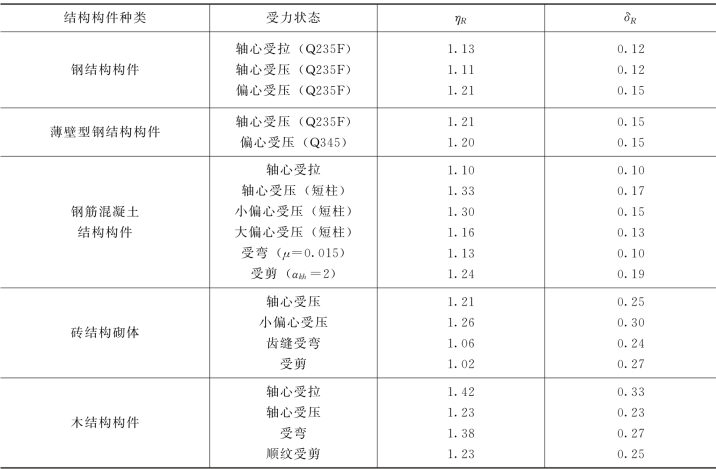
【例4-4】 求Q235钢轴心受拉杆件的统计参数ηR、δR。

解：（1）确定杆件抗力不定性因素的统计参数。

相应于Q235钢，由表4-1知，材料性能不定性变量xm的均值与变异系数为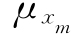＝1.08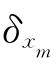，＝0.08；相应于型钢杆件，由表4-2知，几何参数不定性变量xA的均值与变异系数为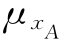＝1.00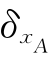，＝0.05；相应于受力模式为轴心受拉构件，由表4-3知，抗力计算模式不定性变量xp的均值和变异系数为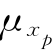＝1.05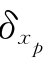，＝0.07。

（2）求统计参数。

对于单一材料构件，由式（4-23）、式（4-24）得到R的统计参数为均值与标准值之比　＝1.05×1.00×1.08＝1.134

变异系数　

【例4-5】 求钢筋混凝土轴心受压构件抗力的统计参数ηR、δR、σR。

由表4-1～表4-3可知：(https://www.xing528.com)

C30混凝土强度fc，（因为，所以，下同）；20MnSi钢筋强度fy，；截面高度h，0.02；截面宽度b，；钢筋截面面积As，0.03；轴心受压构件，。

材料强度和截面尺寸的标准值为＝17.5N/mm2，＝340N/mm2，bK＝30cm，hK＝50cm，配筋率μ＝0.015。

轴心受压构件抗力计算公式

解：由题意知，此构件由两种材料组成，抗力表达式如式（4-25）所示，即

（1）求μR。

其中

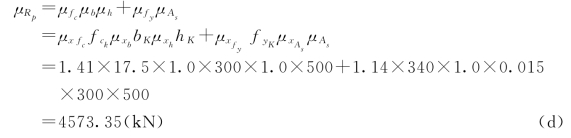
由式（c）有　

（2）求RK。

由式（a）得

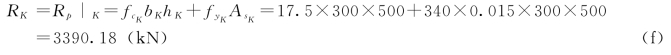
（3）求ηR。

将式（e）、式（f）代入式（4-28）式得到

（4）求δR。

由式（4-27）得

其中　

对式（a）应用式（4-3）得

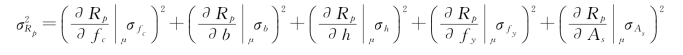
又　

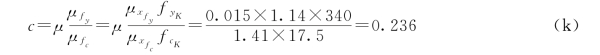
将式（j）、式（k）代入式（i）并注意到

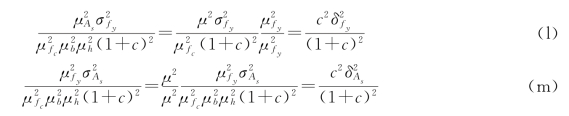
经整理得到

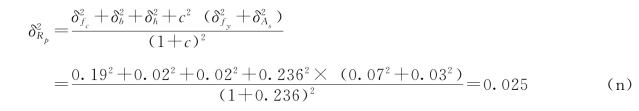
将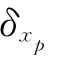＝0.05及式（n）代入式（h）得

（5）求σR。