【例3-1】 某地25年年标准最大风压Qi（N/m2）的记录为
111.4， 138.1， 143.1， 436.7， 352.0，
374.4， 214.2， 198.0， 239.6， 222.5，
314.4， 218.3， 198.0， 160.4， 148.2，
138.1， 204.2， 202.0， 198.0， 118.9，
198.0， 160.4， 126.7， 79.8， 101.2。
求该地设计基准期T＝50年的标准最大风压的统计特征（概率分布函数及统计参数）。
解：（1）计算年标准最大风压统计参数μi、σi。
由点估法得到
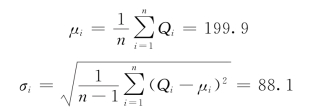
式中n＝25。
（2）统计假设。
统计假设是先假设样本数据服从某种概率分布，再对所假设的概率分布进行统计检验（拟合优度检验）。即：给定信度α并确定相应的接受域下边界（也即否定域上边界），计算检验统计量并作出判断，若统计量在接受域内，表明样本数据以信度α接受假设，所设概型为真。否则重新假设分布类型并检验，直至结果为真为止。
统计检验方法有多种，如K-S检验，χ2检验等。本例采用χ2检验，其基本思想为：
将已知样本数据的全体视为k个互不相容区间上的事件A1，A2，…，Ak。在概型假设成立的条件下，计算各区间上事件Ai发生的概率值Pi＝P（Ai）（i＝1～k），同时计算样本数据落在各区间内的频率
（i＝1～n，mi是样本数据落于区间i内的频数，n为样本总数）与概率pi的差值
，若概型假设为真，则该差值应该很小，否则就大，基于这种思想，利用如下统计量来检验假设是否为真
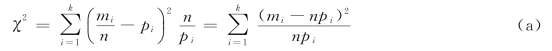
且当样本容量n充分大（一般n≥50）时，不论所设分布为何种类型，只要假设为真，则统计量χ2总是近似地服从自由度为k—r—1的χ2分布（r是待求分布函数中待估参数的个数）。也就是
应该是大概率事件，而
应该是小概率事件。设式（c）的概率为一足够小的数α，有
称α为置信度（简称信度），一般取0.05。
从而由式（d）可得概型检验的拒绝域为
则接受域为
(www.xing528.com)
当由式（a）求出的统计量χ2满足式（f）时，则样本数据以信度α接受所设概率分布类型，即假设为真。α愈小，符合程度愈好。
（3）计算步骤。
1）设样本数据Qi服从极值Ⅰ型分布，其中均值μi、标准差σi未知，均为待估参数，故r＝2。由式（3-13a、b）得
ui＝μi—0.5772αi＝199.9—0.5772×68.69＝160.3
则得
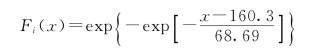
2）取k＝5，即将样本数据分成5个互不相容的区间：A1，A2，…，A5，由式（a）计算统计量χ2，见表3-1。
表3-1 χ2统计量计算表
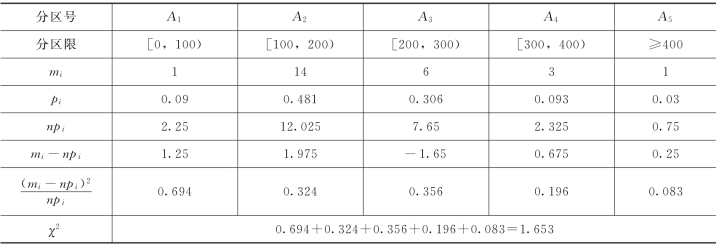
表3-1中，p1＝P（A1）＝P[0≤Qi≤100]＝Fi（100）—Fi（0）
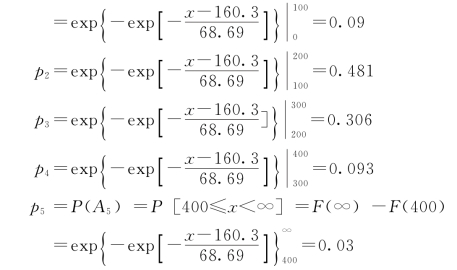
或 P5＝1—P1—P2—P3—P4＝0.03
（4）取信度α＝0.05，k—r—1＝5—2—1＝2，查附表Ⅱ-4得
（2）＝5.991
由表3-1知，χ2＝1.653，可见
χ2＜
（2）
因此，假设为真，即接受该地区年最大风压Qi的分布Fi（x）为极值Ⅰ型的假设。
（5）求设计基准期T＝50年的标准最大风压统计参数。
由式（3-14）知，设计基准期T＝50年的标准最大风压也服从极值Ⅰ型分布，由式（3-17）和式（3-19）可得其均值和标准差为
σT＝σi＝88.1
而参数为
αT＝αi＝68.69
uT＝μT—0.5772αT＝468.6—0.5772×68.69＝429.0
于是，设计基准期T＝50年的标准最大风压QT的概率分布函数为
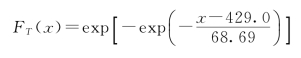
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
