地震荷载分析：底部剪力法！

用振型分解反应谱法求结构的最大地震反应在理论上是精确的，它只在振型组合上存在近似，因此其计算精度较高，但需要计算结构的各阶周期与振型，计算量大而复杂。为便于工程设计采用，在振型分解反应谱法的基础上加以简化，便可得到底部剪力法。

底部剪力法先将地震作用视作等效静力，求出结构底部的最大剪力，再将该剪力加权分配到结构各质点上（权重为质点重量与其离开地面的高度之乘积），作为质点上的地震作用。该法适用于质量与刚度分布较均匀的剪切型结构，且结构高度比较小（≤40m）的情况。

1.基本假定

底部剪力法以如下基本假定为基础：

（1）结构地震反应以第一阶振型反应为主，忽略二阶及其以上的振型反应。

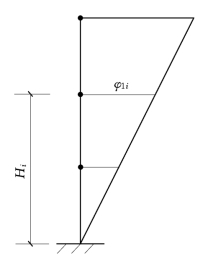
图2-22　第一阶振型分布假定

（2）结构第一阶振型反应为线性倒三角形分布，如图2-22所示，因此任一质点i的振型坐标φ1i与该质点离开地面的高度Hi成正比，即

式中　C——比例常数。

2.底部剪力

按振型分解反应谱法计算公式（2-81），质点i的地震作用为

其中　α1＝α（T1）

注意到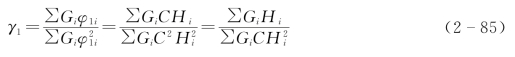　

式（2-84）变为

结构的底部剪力FEK等于各质点地震作用之和，即

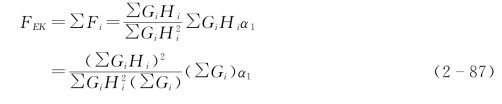
令　

称χ为等效重力系数，GE为结构总重量，则结构底部剪力表达式简化为

对一般建筑结构，各层重量相等，层高相同，可导得χ与层数n之间的关系为

对水利工程中的挡水坝，可简化为多质点结构，这时，式（2-91）中的n也可近似为质点数。显见当n＝1时，χ＝1；而当n＞1时，χ＝0.75～0.90，工程中可近似取χ＝0.85。

3.地震作用分布

由推导过程可知，底部剪力也就是结构各质点上地震作用的总和，可将其分配到各质点上。若将式（2-86）与式（2-87）两边相除，即可得到任意质点上地震作用分布公式为

式（2-92）表明，结构任意质点i上的地震作用与该点的重量及其质点离开地面高度的乘积成正比。

需指出，由于假定第一阶振型φ1i按直线变化，如上求出的Fi与振型分解反应谱的解相比，一般底部偏大，顶部偏小。

在上述推导中忽略了高阶振型反应的影响，当需考虑高阶振型影响时，可在结构顶部附加一个反向集中力ΔFn(www.xing528.com)

式中　δn——与体系结构形式和基本周期有关的系数，一般结构的基本周期愈大，δn值也愈大，但一般δn≤0.3。

于是考虑高阶振型反应影响时，结构任意质点上的地震作用公式为

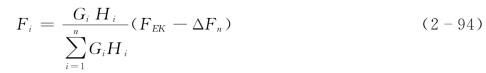
这样，可在底部剪力不变的情况下，调整结构上质点的地震作用分布，减小误差。

【例2-3】 已知结构状况及地震设计反应谱参数同[例2-2]，试用底部剪力法计算地震作用下结构底部最大剪力、各质点地震作用和顶部最大位移。

解：（1）求底部剪力。

对应例2-2中第一阶振型　α1＝0.0798

结构总重量为

GE＝（2.0＋1.5＋1.0）×9.8＝44.1（kN）

结构质点数n＝3，近似取χ＝0.85。则

FEK＝χGEα1＝0.85×44.1×0.0798＝2.991（kN）

FEK与例2-2中V1的百分比误差为

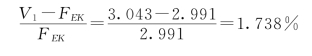
可见，误差很小。

（2）求各质点地震作用。

1）不考虑高阶影响时，有

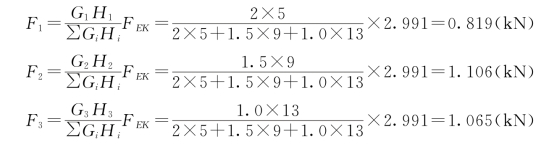
与例2-2中F11、F12、F13的百分比误差分别为

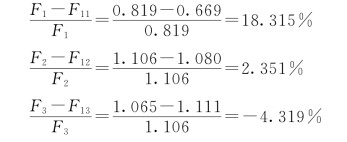
可见，由底部剪力法计算的质点地震作用分布，底部偏大，顶部偏小，由此也可推知，振型分解反应谱法计算的第一阶地震作用分布曲线应是左凸的。

2）考虑高阶影响时，若取δn＝0.05，则

F2＝1.106×0.95＝1.051

F3＝1.065×0.95＝1.012

同上，可求得与例2-2中F11、F12、F13的百分比误差分别为14.010%、—2.759%、—9.783%。

（3）求顶部位移。

不考虑高阶影响，有

与例2-2中u3的百分比误差为