振型分解反应谱法应用与原理

该法是对多自由度体系分解后的各阶振型，利用单自由度体系的地震反应谱求其地震作用（最大地震惯性力），进而求出其在结构内引起的作用效应（内力、变形等），也称最大振型反应，再由振型反应组合来确定结构总地震反应（内力、变形）最大值的一种实用方法。

1.多质点体系的绝对加速度

多质点体系的绝对加速度如图2-20所示。

图2-20　多质点体系绝对加速度图

在地震地面运动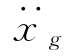（t）激励下，多质点体系的绝对加速度等于其牵连加速度（t）（对每一点相同）与相对加速度（各阶振型加速度反应）之和，用向量表示，即

式中　{a}——体系绝对加速度向量，{a}＝[a1a2…an]T；

ai（i＝1～n）——质点i的绝对加速度。

为使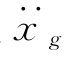与表达式中的系数有统一的形式，现对单位向量{1}变换如下。

先将{1}表示为体系n个独立振型向量{φ1}～{φn}的线性组合，即

式中　αj（j＝1～n）——待定系数。

再以{φi}T[M]左乘式（2-71）两边，同时注意到振型正交性，可知其式右各项中凡i≠j的项为零，只有i＝j项不为零，即

于是可得　

比较式（2-73）与式（2-65）可知

因此式（2-69）可写成

将式（2-75）与式（2-69）代入式（2-70）整理后得到

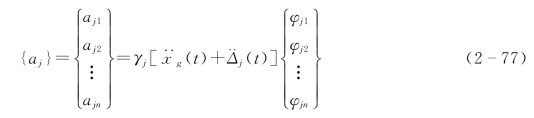
式中{aj}——第j阶振型的绝对加速度，其表达式为

2.多质点体系第j阶振型及其上质点i的地震作用

在振型分解法中，主要任务是计算体系各阶振型的地震作用及其某一振型上各质点的地震作用。

对式（2-77）两边乘以体系的质量矩阵[M]，可得到第j阶振型的地震惯性力，且当其加速度为最大值时的最大地震惯性力即为第j阶振型的地震作用{Fj}，即

式中　{Fj}——第j阶振型地震作用向量，{Fj}＝[Fj1Fj2…Fjn]T；

Fji——第j阶振型上质点i的地震作用。

注意到|（t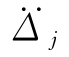）＋（t）|max实际上就是周期为Tj的单自由度体系的加速度反应谱Sa（Tj），故式（2-78）可进一步表达为

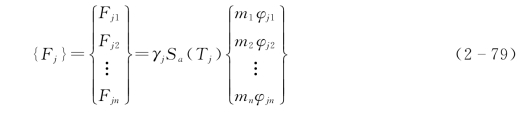
注意到　Sa（Tj）＝kβ（Tj）g＝α（Tj）g且Gi＝mig

式（2-79）可进一步写为

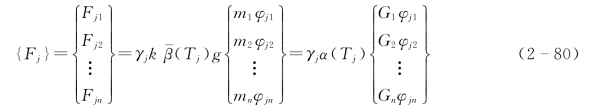
式（2-80）中Fji则为j阶振型上质点i的地震作用，即

3.振型组合

对地震作用引起的结构荷载效应（内力、变形等）分析时，将任一振型的地震作用Fj施加于体系各质点上，由静力分析即可求得结构内相应于Fj的地震作用效应值（表示为Sj）。而当进行各阶振型地震作用的效应组合时，考虑到实际上各阶振型的最大作用效应并非同时发生，将其直接相加，结果一般会偏大。为此，工程中一般采用对各阶振型作用引起的结构效应进行平方和再开方的组合方式，来估算结构的地震作用总效应S，即

【例2-2】 已知某三层剪切结构，如图2-21所示，其各阶周期和振型为：

T1＝0.433s；T2＝0.202s；T3＝0.136s

设计反应谱有关参数：Tg＝0.2s，b＝0.9，αmax＝0.16。图2-21（a）、（b）中，结构质量m1＝2000kg，m2＝1500kg，m3＝1000kg；立柱刚度系数k1＝1800k N/m，k2＝1200k N/m，k3＝600k N/m；长度单位为m。试用振型分解反应谱法求该三层剪切结构在地震作用下的底部最大剪力和顶部最大位移。(www.xing528.com)

解：（1）求地震影响系数α（T）。

因为　T1＞Tg；T2＞Tg；T0＜T3＜Tg　（取T0＝0.1s）

所以　

图2-21　地震作用计算

α（T3）＝αmax＝0.16

（2）求各阶振型参与系数。

同理得　γ3＝0.090

（3）求各阶振型地震作用。

由式（2-80）可得

第一阶　

第二阶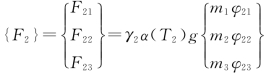　

第三阶　

（4）求各阶振型的底部剪力。

第一阶　V11＝F11＋F12＋F13＝0.669＋1.080＋1.111＝2.860（kN）

第二阶　V21＝F21＋F22＋F23＝1.074＋0.716—0.795＝0.995（kN）

第三阶　V31＝F31＋F32＋F33＝0.697—0.529＋0.141＝0.309（kN）

由振型组合[即式（2-82）]求最大底部剪力为

若只取前二阶振型组合，得到最大底部剪力为

各阶振型的底部剪力百分比为

（5）求顶部位移。

因本例为剪切结构，故忽略立柱挠曲变形产生的侧向位移。

先求第一阶振型地震作用产生的顶部位移u13：

F11只在第一层立柱内产生剪切变形，该变形引起的一层柱顶侧向位移为；F12分别对第一层和第二层立柱产生剪切变形，其引起第一层柱顶侧向位移为，第二层柱顶侧向位移为；F13分别对三层立柱均产生剪切变形，其引起的一层、二层、三层柱顶侧向位移分别为。综上可得

同理可求得第二、第三阶地震作用引起的顶部位移为

由式（2-82）求最大顶部位移为

若只取前二阶振型组合，则为

各阶振型的顶部位移百分比为

由本例结果可得如下结论：结构的低阶振型反应比高阶振型反应大，表明结构的低阶振动更容易被外界激励激发出来，对结构安全造成的影响也较大，往往起主导作用。因此，对单向振动的多自由度结构体系，工程上一般只取前二至三阶振型反应来估计结构的最大地震反应，可以得到工程要求的精度。