多质点体系地震反应分析

在工程实际中，许多结构的质量不能近似地视为集中于结构的一个点上，如多层楼房、质量沿高度接近均匀分布的烟囱等，这时都要将结构处理成多质点体系（图2-18）进行地震反应分析。

1.多质点体系振动微分方程

设由n个质点构成的体系如图2-19所示，在单向水平地面运动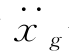—t激励下，一方面随地面运动，一方面相对于地面运动。任意瞬时τ，地面牵连加速度为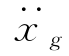（τ），体系相对于地面运动的位移、速度、加速度分别为xi、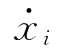、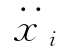（i＝1～n）。

体系中各质点受力如图2-19（b）所示，其中质点mi受力包括惯性力mi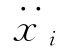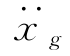（＋）、弹性恢复力ri和阻尼力Ri，其平衡方程为

结构体系的弹性恢复力ri（i＝1～n）与结构的位移x1、x2、…、xn之间应满足刚度方程，即

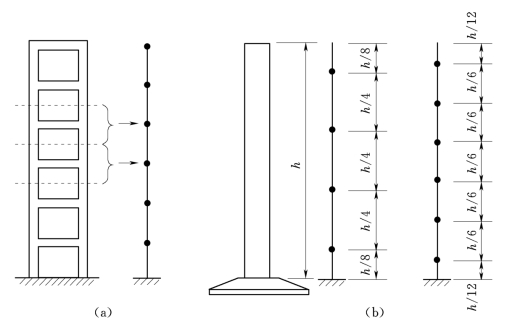
图2-18　多质点体系简图

（a）框架结构的简化；（b）均质结构的简化

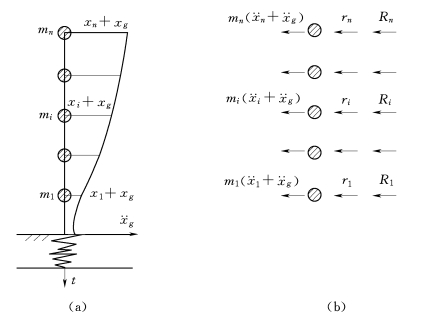
图2-19　多质点体系地震反应

式中　kij——结构的刚度系数，它等于使点j产生单位位移即xj＝1（其他各点的位移保持为零）时在i点需施加的力。

Ri是质点mi的阻尼力。结构采用的材料不同，运动中质点所受的阻尼力不同。结构体系所受的阻尼力Ri（i＝1～n）与结构结点速度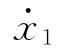、、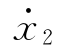…、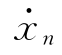也可写成如下形式

式中　Cij——结构的阻尼系数，它等于使点j产生单位速度即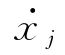＝1（其他各点保持速度为零）时在i点需施加的力。

将式（2-36）与式（2-37）代入式（2-35），可得多质点体系的振动微分方程如下

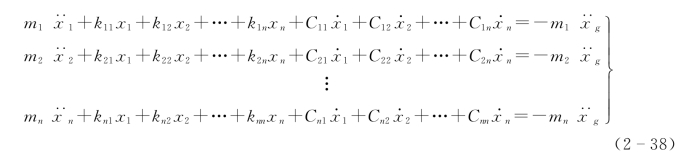
将式（2-38）表示为矩阵形式为

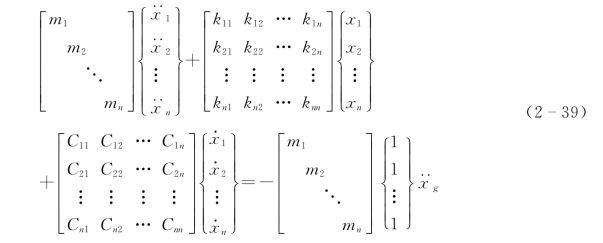
或简写为

式（2-40）即为多质点体系的振动微分方程，式中[M]（对角矩阵）、[C]（对称方阵）、[K]（对称方阵）分别是体系的质量矩阵、阻尼矩阵和刚度矩阵。

2.多质点体系的自振频率与主振型

由于自振频率与主振型是体系的固有特征，与所受荷载无关，故可只考虑相应于式（2-40）的无阻尼自由振动方程

设式（2-41）的解有如下形式

其中

式中　{φ}——体系的位移幅值向量；

φi（i＝1～n）——每个质点的位移幅值，即振幅。

将式（2-42）微分两次，代入式（2-41），并消去公因子sin（ωt＋θ）后得到

式（2-44）是位移幅值向量{φ}的齐次方程，也称特征方程。为得到{φ}的非零解，其系数行列式应为零，即

式（4-45）称为体系的频率方程或特征值方程。将行列式展开，可得到一个关于ω2的n次代数方程，求出此特征值方程的n个根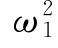、、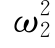…、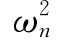*^[1]，即可得出n个自振频率ω1、ω2、…、ωn。把求出的全部自振频率按由小到大的顺序排序而构成的向量称频率向量{ω}，其中最小的频率叫基本频率（简称基频）或第一频率，其中ωi叫第i阶频率。

令{φi}＝[φi1、φi2、…、φin]T为相应于ωi的主振型向量，其中φij为j质点在第i阶振型上的振幅。将ωi及{φi}代入特征方程式（2-44），有

式（2-46）是关于φij（j＝1～n）的n个代数方程组，可解出n个未知量φi1～φin，即为所求第i阶振型上的位移幅值向量。

需指出，由于式（2-46）是一组齐次方程，实际上只有n—1个独立方程，只能求出各点振幅相对值即主振型的形状。欲使各点振幅有确定值，尚需另外补充条件，这样得到的主振型称标准化主振型。常用的标准化方法是规定主振型{φi}中的某个元素为某个给定值，例如规定第1个元素φi1等于1或规定最大元素等于1，本节规定φin＝1（见[例2-2]）。标准化主振型也称振型坐标。

重复上述计算即可得到多质点体系相应于ω1～ωn的n个主振型{φ1}～{φn}。

3.振型正交性

改写式（2-46）成为

(www.xing528.com)

式（2-47）对体系的第j阶自由振动也成立，即

对式（2-47）两边左乘{φj}T，式（2-48）两边左乘{φi}T，则得

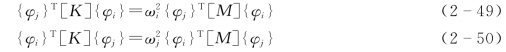
对式（2-49）两边转置，并注意到质量矩阵和刚度矩阵的对称性，即[M]T＝[M]，[K]T＝[K]，则有

将式（2-50）与式（2-51）两边相减，得到

当i≠j时，ωi≠ωj，由式（2-52）得

将式（2-53）代回式（2-51），可得

式（2-52）、式（2-53）即表示，任意两个不同的振型关于体系的质量矩阵和刚度矩阵是正交的。

进一步地，若体系的阻尼矩阵[C]可表示为质量矩阵和刚度矩阵的线性组合，即

其中a、b为常数。对式（2-55）两边左乘{φi}T且右乘{φj}，并注意到式（2-53）和式（2-54），即可得到

可见，振型关于阻尼矩阵也是正交的。多质点体系主振型的上述性质[即式（2-53）、式（2-54）、式（2-56）]称为主振型的正交性。

4.多质点体系地震反应

由振型正交性可知，多质点体系的各阶主振型{φ1}～{φn}是彼此独立的，因此，任意一个位移向量都可按主振型展开，写成各阶主振型的线性组合。于是，对于多质点体系振动微方程式（2-40）的解{x}，现可写成按体系主振型的展开式为

式中　qi（t）——相应于第i阶主振型{φi}的振动函数。

将{x}及其一阶与二阶导数

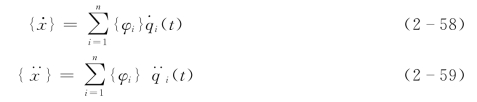
代入式（2-40），可得

将式（2-60）两边左乘{φj}T，并注意到振型的正交性[式（2-53）、式（2-54）和式（2-56）]，可知在式（2-60）左边的n项中，除第j项外，其余各项均为零，即有

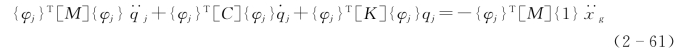
将式（2-61）两边同时除以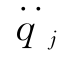（t）的系数，得到

其中　

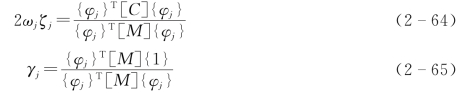
式中　ζj——体系第j阶振型阻尼比（简称j阶阻尼比）；

γj——第j阶振型参与系数。

比较式（2-13）可知，式（2-62）实际上是圆频率为ωj、阻尼比为ζj的单自由度体系的振动微分方程，唯式（2-62）右端的地面运动项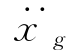需乘以振型参与系数γj。因此，仿式（2-13），式（2-62）的解可表达为

式中　Δj（t）——圆频率为ωj、阻尼比为ζj的单质点体系在水平地面运动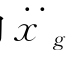激励下相对于地面的地震位移反应，类同于单质点体系的式（2-16）。

同理求得q1（t）～qn（t），代入式（2-57）则得多质点体系的地震位移反应

式中　{xj}——体系按主振型{φj}振动的位移反应，称第j阶振型地震反应（相对于地面）。

将式（2-67）微分一次、二次可得到体系速度反应{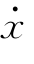}和加速度反应{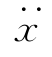}如下

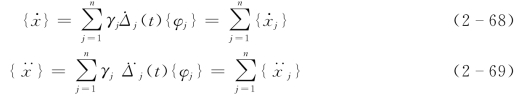
式中{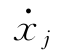}、{}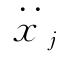——体系第j阶振型速度反应和加速度反应。

式（2-67）～式（2-69）表明，n个自由度（n个质点）体系的地震反应可分解为相当于n个独立的单自由度体系的振型反应的叠加，这种分析多质点体系地震反应的方法称振型分解法。