单质点体系地震反应：地震荷载动力分析与可靠度设计原理

对于形如水塔、一层楼房之类的结构，体系的质量集中于顶部，塔身、墙柱等简化为弹性杆，则可视为单质点体系，如图2-10所示。

严格而言，地震地面运动是三维运动，但若结构处于弹性状态，可将三维地面运动对结构的影响分解为三个一维地面运动对结构的影响之和。为此，本节只讨论单向水平地震地面加速度过程对单质点体系的影响。

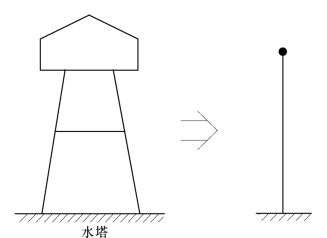
图2-10　单质点体系简图

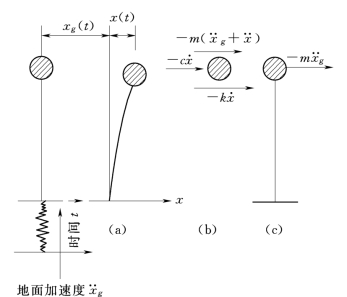
图2-11　单质点体系地震反应

1.振动微分方程

设单质点体系地震反应如图2-11所示，其质量为m，系统阻尼系数为c，弹性杆刚度系数为k，在体系所在平面内受地面传来的水平加速度激励过程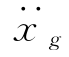—t，任意τ瞬时，体系所受加速度激励量值为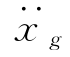（τ）（牵连加速度），激励引起的质点相对于地面的位移x（τ），速度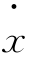（τ），加速度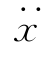（τ），此时质点m受三种力的作用：

惯性力　

阻尼力　

弹性恢复力　

由质点上力系平衡可得单质点体系振动微分方程为

将上式两边除以m，得到标准化形式

式中　

对于连续作用的地面加速度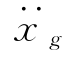—t，以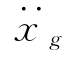（τ）dτ代替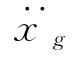（τ），则式（2-13）成为(www.xing528.com)

式中　dτ引起的质点位移微分、速度微分和加速度微分。

式（2-14）即为单质点体系（微分形式）振动微分方程。

2.地震反应

注意到体系运动初始条件：x（0）＝0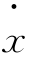，（0）＝0，方程式（2-14）的解为

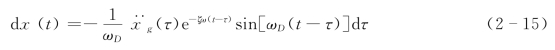
式（2-15）即是在地面运动激励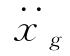（τ）dτ作用下体系位移反应的微分形式，对式（2-15）在0～t内积分，可得体系总位移反应为

其中　

式（2-16）称杜哈密（J.M.C.Duhamel）积分，它即是用积分形式表达的单质点体系相对于地面的地震位移反应，其中ω为无阻尼体系自由振动圆频率；ζ为阻尼比；ωD为有阻尼体系自由振动的圆频率。一般工程结构ζ值很小，约在0.01～0.1之间，忽略其影响，有ωD≈ω。

将式（2-16）对时间t微分一次、两次，可得到体系相对于地面的速度反应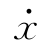和加速度反应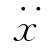

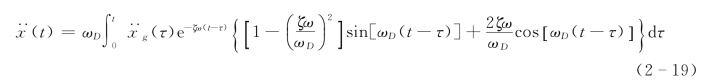
忽略阻尼影响时，ζ＝0，ωD≈ω，上两式简化为

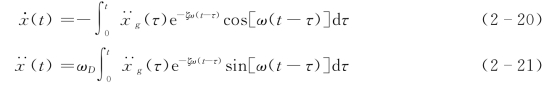
在地震地面运动激励下，单质点体系一方面随地面运动，另一方面相对于地面产生运动位移、速度及加速度反应，其在绝对运动中的加速度为