本书提出了一种新型超级电容系统分数阶模型，其模型结构如图6−15所示。该模型由一个串联电阻Rs、一个并联电阻、一个CPE和一个Warburg−like单元组成。
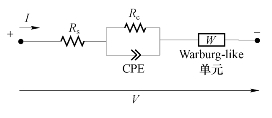
图6−15 超级电容器分数阶模型
CPE的阻抗可以表示为
式中，C描述CPE的容抗特性，s表示复变量，α（α∈R，0≤α≤1）是分数阶因子，当α=1时，CPE为普通电容，其中分数阶α在模型参数辨识过程中是待定参数之一，允许其变化提高了模型的模拟能力。与CPE并联的电阻Rc用于描述超级电容系统内部电荷扩散和重分布的动态过程。Warburg−like单元用于代表超级电容的主要容抗特性，其阻抗表示为
式中，W表示容抗因子，β（β∈R，0≤β≤1）描述电容量分布。值得注意的是，当β=0时，Warburg−like单元表示电阻；当β=1时，Warburg−like单元表示理想电容。
最终，得到超级电容阻抗模型：
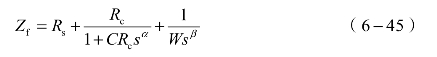
通过拉普拉斯变换，得到超级电容系统分数阶模型传递函数：
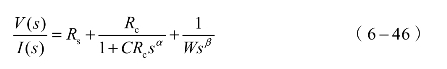
式中，V（s）表示超级电容端电压，I（s）表示充电电流。式（6−46）可以进一步转化为
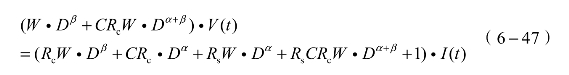(www.xing528.com)
由于只有在特殊情况下才能得到方程（6−47）的解析解，因此，数值方法成为求解分数阶模型的关键。其主要思想是通过多项式差值、高斯差值或分段分数阶多步法等方法，用整数阶微分运算近似代替分数阶微分运算。由于GL定义方法具有直观、简洁等优点，在本书用于实现超级电容系统模型连续状态表达式的离散化。观测方程（6−47）可知，待定模型参数为
基于短期记忆原则，我们利用高阶差分方程近似计算式（6−47），这里仅利用附近时间点进行近似计算，有效减小了运算量。相应的近似结果为
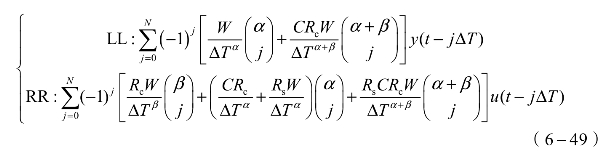
式中，LL和RR分别表示方程左右两边算子；N表示近似的离散时间点数；ΔT表示采样时间；y（t）和u（t）分别表示输出电压V（t）和输入电流I（t）。
基于不同温度下的FUDS试验数据，利用遗传算法离线估计分数阶模型的参数，结果如表6−5所示。在20℃下，模型预测输出与试验实测数据对比如图6−16所示。在初期，动态模型预测电压与实测电压存在较大偏差，证明了该模型的局限性。而分数阶模型则可以在整个实验时间段内准确描述超级电容的动态电压特性。
为了进一步验证分数阶模型的精度，在频域内与动态模型以及EIS测试阻抗谱数据进行了对比，对比结果如图6−17所示。很明显，在−40℃和−20℃下，分数阶模型与动态模型均可以准确描述超级电容的动态特性。但是，在0℃，20℃和40℃下，分数阶模型依然保持着良好的模型精度，而动态模型的低频精度较差，这是由于在这些温度下阻抗谱曲线斜率陡然增大，而整数阶模型没有能力完全捕捉这样的变化。也就是说，分数阶模型可以在全工作温度范围内精确代表超级电容的动态特性，而动态模型则在冰点以上温度精度相对较差，凸显了分数阶模型的优越性。
表6−5 超级电容分数阶模型参数
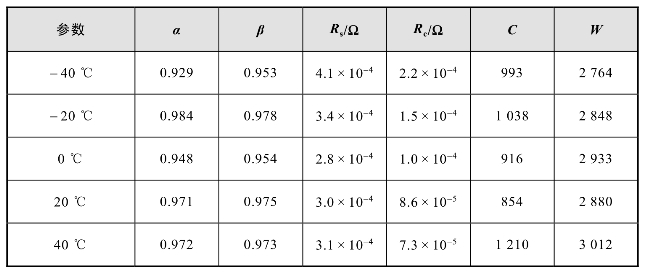
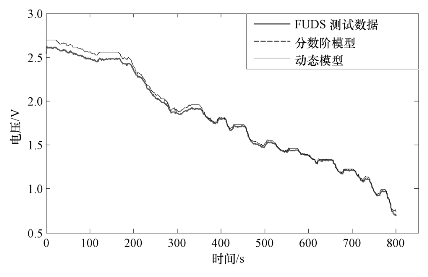
图6−16 20℃ FUDS工况模型精度比对
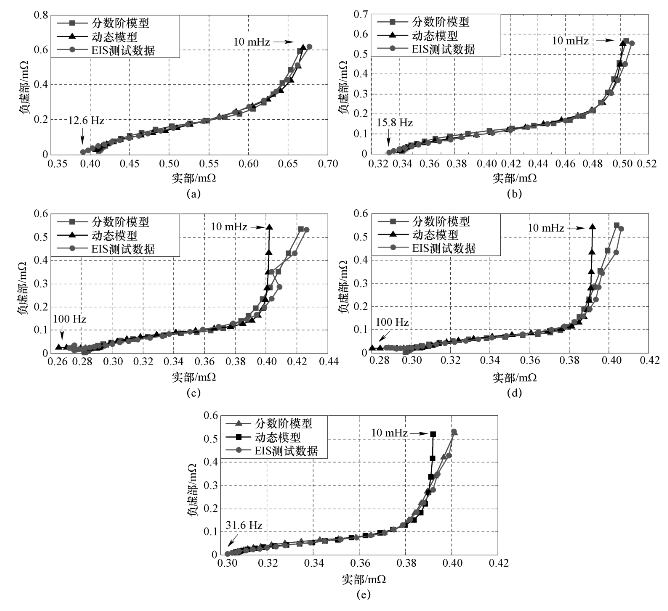
图6−17 100%SOC状态下，分数阶模型与动态模型阻抗谱对比
（a）−40℃；（b）−20℃；（c）0℃；（d）20℃；（e）40℃
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
