环状管网水力计算，给水排水工程成果

一、环状管网的计算原理

（一）环状管网计算的基础方程

1.管段数、节点数和基环数之间的关系

对于任何环状管网，管段数P、节点数J（包括泵站、水塔、高地水池等水源节点）和基环数L之间存在下列关系：

如图5-9（a）所示的环状网，P=13，J=10，L=4，符合（5-23）式的关系。在图5-9（b）中，高峰供水时，由水泵和水塔同时向管网供水，计算时可增加虚节点0和虚管段0-1、0-10，并构成虚环V，此时P=15，J=11，L=5，仍符合（5-23）式的关系。

对于树状网，因环数L=0，故P=J-1。

2.环状管网计算的基础方程

环状管网计算时必须满足质量守恒定律和能量守恒定律。由这两个定律得出的连续性方程和能量方程是环状管网计算的基础方程。

连续性方程是指对任一节点来说，流向该节点的流量必须等于流出该节点的流量，即应满足式（5-6）表达的节点流量平衡关系。若某个管网有J个节点，因其中任一节点的连续性方程可由其余方程导出，故可写出J-1个独立的连续性方程：

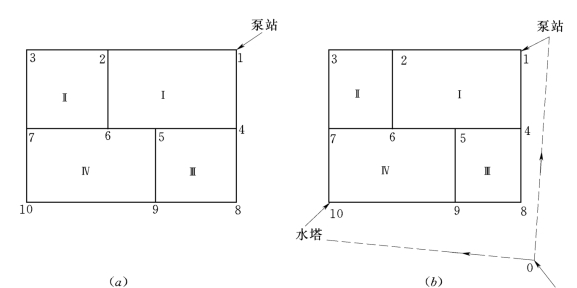
图5-9　环状网的管段数、节点数和环数

（a）单水源管网；（b）多水源管网

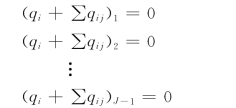
能量方程是指在环网的任一闭合环内各管段水头损失的代数和等于零，即：（5-24）

本书规定，水流沿顺时针方向的管段，水头损失为正；沿逆时针方向的管段，水头损失为负。若某个管网有L个环，则可列出L个能量方程：

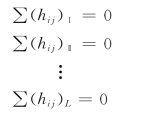
式中：Ⅰ、Ⅱ、…、L分别为管网中各环的编号。

根据水头损失与流量的关系式（5-15），能量方程还可写为

（二）环状管网计算的基本方法和原理

环状管网计算时，节点流量、管段长度、管径和阻力系数等均已知，需要求解的是管网各管段的流量和水头损失（或节点水压）。求解时可采用解环方程组、解节点方程组和解管段方程组等3种方法。

1.解环方程组法

该方法是以管网中每环的校正流量为未知变量进行求解的方法。

该法首先对管网进行初步流量分配，分配后各节点已满足连续性方程，但由初步分配的管段流量所求出的管段水头损失，并不一定同时满足L个环的能量方程，即各环的水头损失代数和不一定等于零，这样各环就产生了水头损失闭合差（即水头损失的代数和）Δh，为此必须调整各管段的流量，方法是求出各环的校正流量Δq，将原来流量小（水头损失小）的管段增加Δq，原来流量大（水头损失大）的管段减少Δq，使调整后顺时针和逆时针方向各管段中的水头损失之和趋于相等。流量调整后再计算检验各环是否满足能量方程，若不满足，则再求出各环的第二次校正流量Δq，如此反复调整，直至各环满足能量方程（Δh小于规定的数值），从而得出各管段的流量和水头损失。

由于环数少于节点数和管段数，故环方程数目较节点方程和管段方程数目少，因而解环方程组法是手工计算的主要方法，而哈代-克罗斯（Hardy-Cross）法是其中最常用的一种方法，这种方法将在环网计算中详细介绍。

2.解节点方程组法

该方法是以管网中各节点水压值为未知数进行求解的一种方法。节点水压求出后，就可求出两节点间管段的水头损失，再根据流量和水头损失之间的关系求出各管段流量。解题思路如下：

列出J-1个节点连续性方程，由于流量和水头损失及节点水压之间存在下列关系：

可将J-1个连续性方程中的管段流量qij用管段两端的节点水压Hi和Hj表示，这样，在J-1个连续性方程中就只含有J-1个节点水压未知数（在J个节点中，必有一个节点的水压是已知的，如控制点或水源点），解此方程组，就可得出各节点水压值，从而求出各管段水头损失和管段流量。

由于上述J-1个节点方程是非线性的，无法直接求解，因而实际求解时往往采用逐步逼近法，工程上常用的方法为哈代-克罗斯迭代法，具体步骤如下：

（1）根据已知的控制点的水压标高（或泵站的水压标高），假定其他各节点的初始水压，并应满足能量方程。假定的初始水压越接近实际水压，则计算时收敛越快。

式中：Δqi为任一节点i的流量闭合差。

（4）除水压已定的节点外，其余各节点均按各自的ΔHi校正水压。根据新的水压，重复上述计算步骤，直到所有节点满足连续性方程，即Δqi达到预定的精度为止。

应用计算机求解给水管网时，往往采用解节点方程组法，程序设计请见其他有关书籍。

3.解管段方程组法

该方法是以管网中各管段流量为未知数进行求解的一种方法。其解题思路是，同时列出J-1个连续性方程和L个能量方程，共计P个方程，含有P个未知的管段流量，解此联立方程组，即可求出管网中P个管段的流量。由各管段流量可求出各管段的水头损失。

因连续性方程是线性方程，而能量方程是非线性方程，故上述联立方程组无法直接求解，为此，可用线性理论法先将L个能量方程转化为线性方程，方法是设管段的水头损失hij近似表示为

式中：sij为管段摩阻；qij（0）为管段的初始假设流量；cij为系数；qij为待求的管段流量。

解管段方程组法方程数目多，故宜用计算机进行计算。

二、环状管网的水力计算方法

本部分主要介绍解环方程组法。

（一）环状管网的计算步骤

（1）环状管网定线后，确定管网节点和节点间各管段的计算长度。按照最高日最高时流量计算管网的集中流量、比流量、沿线流量和节点流量。

（2）初步拟定环网各管段的水流方向，应使转输流量沿最短路线供至最远地区。根据输入管网的总流量，并考虑供水可靠性要求，对整个管网进行流量分配，此时各节点应满足节点流量平衡关系。

（3）根据初步分配的流量，按平均经济流速，也可按界限流量或经济管径与流量的关系式（后二者将在本章第八节中介绍），选择市售标准规格的管径。另外确定管径时还应满足消防、事故和转输时的水量、水压，因此某些管段的管径要适当放大。

（4）进行管网水力计算，即解环方程组，也就是在按初步分配流量确定管径的基础上，计算各管段的水头损失，若各环不能同时满足能量方程，则应重新分配各管段的流量，反复计算，直到同时满足连续性方程和能量方程时为止。这一计算过程称为环网平差。环网平差是环网计算的中心工作，通过平差可以求得各管段的真实流量。环网平差的具体步骤如下：

1）根据每一管段的管径、流量、管长，计算每一管段的水头损失hij。

2）按照水头损失正负号的规定（水流顺时针时为正，逆时针时为负），计算各环水头损失闭合差Σhij。

3）当某个环的Σhij≠0时，说明原来假定的管段流量有误差，必须进行修正。根据Σhij的大小和正负号，计算每一环流量的修正值Δq。

4）重新计算每个管段修正后的流量。

5）在管径不变的基础上（若管径选得不合理时可以改变），重复（1）～（4）步，直到每个环的闭合差达到要求为止。一般手工计算时，小环的闭合差小于0.5m，大环的闭合差小于1.0m。计算机计算时，闭合差可以达到任何要求的精度，但可采用0.01～0.05m。

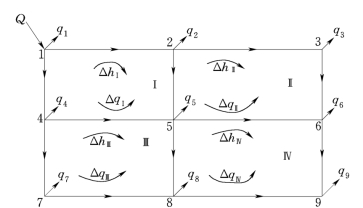
图5-10　环状管网的校正流量计算

（5）根据平差的最后结果，计算各管段的水头损失，并计算水泵扬程和水塔高度，画出管网等水压线图。

（二）解环方程组的常用方法

1.哈代-克罗斯法

此法也称洛巴切夫（В.Т.Лобачев）法，是渐进法的应用。下面以图5-10为例，说明哈代-克罗斯法的计算方法。

设管网中各节点流量已确定，各管段初步分配的流量qij已拟定，并根据qij求得了所有管段的管径和管段摩阻sij。取水头损失公式h=sqn中的n=2，计算各环中水头损失的闭合差Δh：

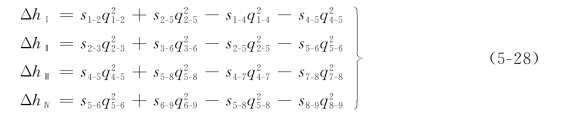
若各环的Δh≠0，说明分配的流量不能满足能量方程。如Δh＞0，表明顺时针方向的流量分配过多；如Δh＜0，表明逆时针方向的流量分配过多。这样在Δh≠0的环内就必须引入校正流量Δq来校正环内各管段的流量。校正流量Δq的方向应和水头损失闭合差Δh的方向相反，校正后应使Δh=0。

现假设4个环的校正流量分别为ΔqⅠ、ΔqⅡ、ΔqⅢ和ΔqⅣ，方向均与各环的Δh相反。对各管段的流量进行修正：在流量过大的管段上减去校正流量；在流量过小的管段上加上校正流量。两环相邻的共有管段应同时考虑两环的校正流量。流量校正后，列出4个环的能量方程：

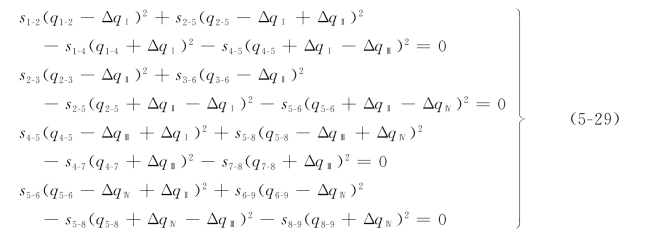
上式括号内为在初步分配流量时，在环Ⅰ中产生的水头损失闭合差ΔhⅠ。因此各环的能量方程整理如下：

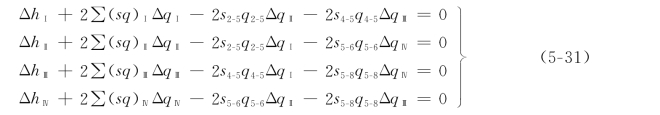
式中：Σ（sq）i为该环内各管段的|sq|值总和。(www.xing528.com)

解上述方程组，就可求出待求的校正流量Δqi，但环数目多时，计算是很繁琐的。哈代-克罗斯法采用以下的逐次渐进法，求得Δqi值。

为简化计算，忽略环与环之间的相互影响，即每环调整流量时，不考虑邻环校正流量的影响，亦即将式（5-31）中的后两项忽略，这样可得到基环的校正流量公式：

根据初步分配的流量和各环的水头损失闭合差，可以得到第一次的校正流量Δqi（0），据此调整各管段的流量，凡是流向和校正流量方向相同的管段，加上校正流量，否则减去校正流量。每次调整流量后，可以自动满足节点流量平衡关系。第一次校正后的管段流量qij（1）为

式中：qij（0）为某管段初次分配的流量；Δqs（0）为本环的初次校正流量；Δqn（0）为邻环的初次校正流量。

按qij（1）再进行计算，如闭合差仍未达到要求的精度，则再求出第二次的校正流量，反复计算，直到每环的闭合差达到要求为止。

环网平差完成后，根据控制点的地形标高和要求的最小服务水头，可计算出控制点的水压标高，再根据各管段的水头损失，可逐一推出各节点的水压标高。根据各节点的水压标高，可在管网平面图上用插值法按比例绘出等水压线（若泵站提供的水压比要求的水压大ym，则每一节点的实际水压均应加ym）。由各节点的水压标高减去地面标高得到各节点的自由水压标高，在管网平面图上也可绘出等自由水压线。图5-11为某管网的等水压线示意图。

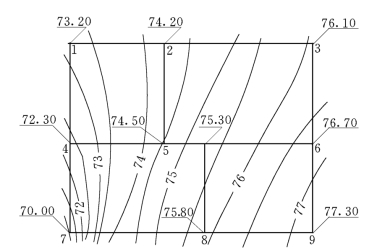
图5-11　等水压线示意图

2.最大闭合差的环校正法

该法与哈代-克罗斯法的不同之处在于，不必逐环平差，而选闭合差大的环或构成大环进行平差。应用此法可以减少平差工作量。

该法首先按初步分配的流量求出各环闭合差的大小和方向，然后选择闭合差大的一个环或将闭合差较大且方向相同的相邻基环连成大环进行平差。对于环数较多的管网，有时可以连成几个大环进行平差。平差后，和大环闭合差异号的各邻环，闭合差会同时减小，这样可以加快平差速度。但要注意的是，决不能将闭合差方向不同的几个基环连成一个大环，否则将出现和大环闭合差方向相反的基环的闭合差反而增大的情况，致使计算不能收敛。

以图5-12为例，各基环闭合差方向如图所示。假设环Ⅰ、Ⅱ、Ⅳ的闭合差较大，由于它们的方向相同，故可连成一个大环进行平差。大环闭合差的方向与这几个小环相同，为顺时针方向，闭合差值等于这几个小环闭合差值之和，即

图5-12　最大闭合差的环校正法

校正流量值Δq大可按式（5-33）去求，有经验者可凭经验拟定。Δq大与Δh大方向相反，所以为逆时针方向。在大环的顺时针方向管段减去校正流量，逆时针方向管段加上校正流量。流量调整后，大环闭合差将减小，相应地环Ⅰ、Ⅱ、Ⅳ的闭合差随之减小。同时，与大环相邻的、闭合差与大环相反的环Ⅲ、环Ⅴ，因受到大环流量校正的影响，流量也将发生变化，如环Ⅲ中的管段3-7减小了校正流量；环Ⅴ中的管段6-7增加了校正流量；管段6-10减小了校正流量；其结果是环Ⅲ、环Ⅴ的闭合差都减小，因而环网平差工作量减小。如第一次校正后，各环的闭合差仍未达到要求，则按校正后的闭合差大小和方向重新选择大环继续计算，直到各环闭合差达到要求为止。

三、多水源管网的计算

前面主要讨论了单水源管网的计算方法。对于供水区域不大、供水安全性要求不高的地区可采用单水源供水。但对于大中城市，若有不止一个可利用的水源时，应尽量采用多水源供水，以加强供水的安全性。

（一）多水源供水的特点及虚环概念

多水源（包括水塔、高地水池等）管网与单水源管网的计算基本方程是相同的，即应满足连续性方程和能量方程，但同时又有其特殊性：每一水源的供水量，不仅取决于管网所需水量，还随各水源的水压及管网中的水头损失而变化，因而各水源之间存在流量分配问题。这样在多水源供水时，就可能存在两种工作情况（以设置对置水塔的图5-13为例）。

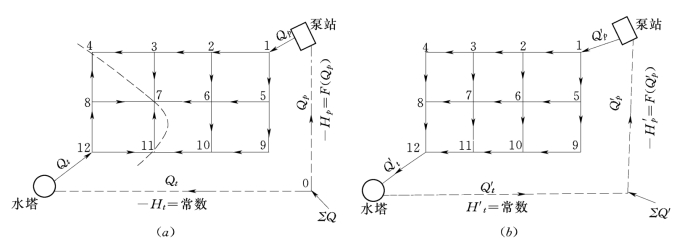
图5-13　对置水塔（两水源）的工作情况

（a）最高用水时；（b）最大转输时

（1）在最高用水时，由几个水源同时向管网供水，各水源有各自的供水区，形成供水分界线。由于假定沿线流量都在节点出流，所以供水分界线必须通过节点。在供水分界线上水压最低，因此，供水分界线上的节点流量，一部分由泵站供给，一部分由水塔供给。在图5-13（a）中，虚线为供水分界线。

（2）在设置对置水塔时，由于一天内有若干小时二级泵站的供水量大于用水量，多余的水通过整个管网转输入水塔储存，形成最大转输供水情况，这时两水源管网成为单水源管网，不存在供水分界线，如图5-13（b）所示。

无论何种工作情况，都可应用虚环的概念将多水源管网转化为单水源管网。虚环就是首先设置一个虚节点（位置可任意选定），假设它为各水源供水量的汇合点，然后将各水源与虚节点用虚线连接成环，如图5-13所示。在图中，虚环由虚节点0、0点到泵站和水塔的虚管段以及泵站到水塔之间的实管段（泵站-1-5-9-10-11-12-水塔的管段）组成。这样多水源管网就可看成是只从虚节点0供水的单水源管网。

从图5-13中看出，两水源供水时可形成一个虚环。一般地，虚环数等于水源数减1。

（二）虚环计算

在虚环计算中应满足下列条件。

1.满足连续性方程

在最高用水时，泵站和水塔均向管网供水。因此，从虚节点流向泵站的流量即为泵站的供水量Qp，从虚节点流向水塔的流量即为水塔的供水量Qt。在最大转输时，泵站的供水量Q′p除满足管网的需求外，多余的水量Q′t成为转输流量进入水塔，并经虚管段流向虚节点0。无论在何种工作情况下，虚节点都应满足节点流量平衡关系，即满足连续性方程。设流量正负号的规定与前面的规定相一致，则两种工作情况下虚节点0的流量平衡方程如下（见图5-13）：

（1）最高用水时：

式中：Qp、Qt分别为最高用水时水泵和水塔的供水量；ΣQ为最高用水时管网用水量。

（2）最大转输时：

式中：Q′p为最大转输时泵站的供水量；Q′t为最大转输时进入水塔的流量（即转输流量）；ΣQ′为最大转输时管网用水量。

2.满足能量方程

由于虚管段中实际上没有流量，因此不考虑摩阻，只考虑按某一基准面算起的水泵扬程和水塔水压。水压符号规定如下：流向虚节点的管段，水压为正；流出虚节点的管段，水压为负。两种工作情况时虚管段的水压符号见图5-13，虚环应满足的能量方程如下（见图5-13）。

（1）最高用水时：

式中：H′p为最大转输时的泵站水压，kPa或m；Σh′为最大转输时从泵站到水塔的总水头损失，kPa或m；H′t为最大转输时的水塔水位标高，kPa或m。

3.各水源供水至供水分界线处的水压应相同

各水源到分界线上节点间的水头损失之差应等于水源的水压差，如式（5-37）和式（5-38）所示（两式也可见图5-14）。

以上介绍了虚环计算时应满足的条件。多水源管网计算时应把虚环和实环作为一个管网整体，即虚环和实环同时计算。管网闭合差和校正流量的计算方法同单水源管网。

四、管网的核算条件

图5-14　对置水塔水压与水头损失平衡情况

1-最高用水时；2-最大转输时

管网的管径和水泵扬程，是按设计年限内最高日最高时的用水量和水压要求确定的，但还应核算由此确定的管径是否能满足其他不利的特殊用水情况下的用水量和水压要求。特殊用水情况主要指消防供水、最大转输供水及最不利管段发生故障时的供水情况。通过核算，若不能满足要求，则应适当放大管网中个别管段的管径，或另选合适的水泵。

（一）消防供水时的管网核算

室外消防给水一般采用低压给水系统，即管道的压力应保证灭火时最不利点处的消火栓水压力不小于10m水柱（从地面算起）。因而一般消防时比最高用水时所需服务水头要小得多。但因消防时通过管网的流量增大，各管段的水头损失也相应增大，因此按最高用水时确定的水泵扬程有可能不满足消防时的要求，这样在消防供水时就需要对管网进行核算。

1.室外消防用水量

城镇、居住区室外消防用水量，应按同一时间内的火灾次数和一次灭火用水量确定。同一时间内的火灾次数和一次灭火用水量，不应小于表3-5的规定。

此外，工厂、仓库和民用建筑对室外消防用水量也有要求，也按同一时间内的火灾次数和一次灭火用水量计算室外消防用水量。同一时间内的火灾次数不应小于表3-6的规定，建筑物的室外消火栓用水量不应小于表3-7的规定。

对于堆场、储罐等其他特殊场地及装置的消防用水量的要求详见《建筑设计防火规范》。

按城镇、居住区和按工厂、仓库及民用建筑两种方法计算的室外消防用水量有可能不一致，此时应取其较大者作为城镇的室外消防用水量。

2.消防供水时的管网核算方法

（1）首先确定同时起火次数和消防用水量。然后在管网的控制点增加一个集中的消防流量。如按照消防要求同时有两处及两处以上起火时，则应综合考虑安全和经济等方面的因素，将消防流量一处放在控制点处，其他放在离二级泵站较远或靠近大用户的节点处。

（2）以最高日最高时用水量确定的管径为基础，将最高时用水量与消防流量相加后进行流量分配。

（3）进行管网平差，求出消防时的管段流量和水头损失。

（4）计算消防时所需要的水泵扬程。若按最高用水时选择的水泵能够满足消防时的流量和扬程要求，则管网管径和水泵不需进行调整。若不能满足要求，则可适当放大个别管段的管径，以减小水头损失。若消防和最高用水时的水泵扬程相差很大，则需设置专用消防泵。

（二）最大转输时的管网核算

设置对置水塔的管网，当泵站供水量大于管网用水量时，多余的水量要通过整个管网转输进入水塔储存，最大转输时管网的水头损失有可能比最高用水时的水头损失大。因此，设置对置水塔的管网，应按最大转输时的流量进行管网核算。

核算时，某些节点出流的集中流量按实际情况确定，然后求出最大转输时各节点的生活流量。由于各节点生活流量随用水量的变化成比例地增减，因此最大转输时各节点的生活流量可按下式计算：

节点流量确定后，按管网最大转输时的流量进行分配和管网平差，求出各管段流量、水头损失和所需要的水泵扬程，并对原来选择的水泵进行校核。

（三）最不利管段发生故障时的管网核算

管网管线损坏（发生事故）时必须马上检修，检修期间供水量允许减少。城市管网事故时的流量一般为最高时流量的70%，工业企业的事故流量按有关规定确定。事故时管网流量虽然减少，但因某个管段损坏不能通过流量，故加大了其他管段的负担，因而管网总水头损失有可能增大，所以也必须进行管网核算。一般按管网的最不利管段损坏而需断水检修的情况进行核算。核算时各节点流量为最高时流量的70%。

核算后，水泵不能满足事故要求时，可放大某些连通管的管径，或重新选择水泵。