桥梁工程概论：墩台设计与计算方法

1.墩台的设计荷载及其组合

在进行墩台设计时，首先应确定作用在墩台上的荷载，详见第三章。

各荷载和外力的计算值，应采用墩台在正常情况下结构上有可能出现的最大荷载值，可依据桥规和有关资料计算。土压力计算一般采用库伦主动土压力公式，活载土侧压力的计算，铁路桥台要考虑其沿横桥向的分布宽度，而公路桥台则按横桥向全宽均匀分布处理。

墩台所受的各项荷载中，除恒载外，其他各项荷载的数值是变化的且不一定同时发生。因此在设计墩台时，就需要针对不同的验算项目，确定各种可能的最不利荷载组合，对墩台加以验算，确保设计安全。在荷载组合当中，车辆活载起着支配作用。

重力式桥墩计算中，一般需验算墩身截面的强度、墩身截面的合力偏心距及桥墩的纵向及横向稳定性。为此，可拟订如下几种可能的荷载组合：

（1）按在桥墩各截面上可能产生的最大竖向力的情况进行组合。它用来验算墩身强度和基底最大应力。因此，应在相邻两跨满布活载的一种或几种，以使墩身或基底产生最大压应力。活载布置分别见图7.39（a）（铁路桥梁称双孔重载）和图7.40（a）（公路桥）。

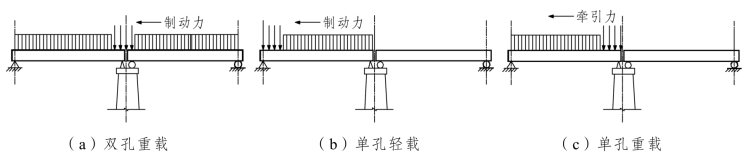
图7.39　铁路桥墩活载布置图式

图7.40　公路桥墩活载布置图式

（2）按桥墩各截面在顺桥向可能产生的最大偏心和最大弯矩的情况进行组合。它是用来验算墩身强度，基底应力、偏心及桥墩的稳定性。因此，应在跨径较大的一孔上布置活载的一种或几种，以及可能产生的制动力、纵向风力、支座摩阻力等。活载布置见图7.39（b）、（c）（铁路桥，分别称单孔轻载、单孔重载）和图7.40（b）（公路桥）。

（3）按桥墩各截面在横桥向可能产生最大偏心和最大弯矩的情况进行组合。它是用来验算横桥向的墩身强度、基底应力、偏心及桥墩的稳定性。因此，对于铁路桥墩，应在相邻两跨布置空车以产生横向摇摆力，而竖向力又不大，称为双孔轻载（也称双孔空车）；对于公路桥墩应注意将活载偏于桥面的一侧布置，此外还应考虑其他荷载如横向风力、流水压力等，如图7.40（c）所示。

桥台的荷载组合也和桥墩一样，依据不同的验算项目进行各种可能的荷载组合。由于活载既可布置在桥跨结构上，也可布置在台后，在确定荷载最不利组合时，通常按台后布置活载而桥上无活载（最大水平力和最大后端弯矩组合），桥上满布活载（最大前端弯矩），桥上、台后同时布置活载（最大竖向力组合）等几种不利情况，分别进行组合与验算，见图7.41示意。

图7.41　桥台活载布置图式

2.墩台的验算内容

桥梁墩台的设计过程是，首先选定墩台形式及拟订各部分尺寸，然后确定各项外力并进行最不利荷载组合；选取验算截面和验算内容，计算各截面的内力，进行配筋和验算。

墩台验算的目的在于确定经济合理的尺寸，并保证其在施工和使用阶段的安全。就重力式墩台来说，应满足两方面的要求：一是墩台本身有足够的强度和稳定性，并且不出现过大的开裂，为此，应进行强度验算、稳定性验算及偏心验算。二是桥墩或桥台作为一个整体，不致发生不容许的变位，为此，就扩大基础（见本章第三节）而言，应进行基底应力验算、整体稳定性验算（包括倾覆稳定性和滑动稳定性）。第二个方面的验算属于墩台的基础部分。此外，对于较高的桥墩，需验算墩顶弹性水平位移；对超静定桥梁结构，应验算基底沉降量；对钢筋混凝土墩台，要进行配筋设计和验算。以下简要介绍重力式墩台的验算内容，凡验算式中的荷载值（竖向力，弯矩）均指最不利荷载组合值。

砌体（或圬工）结构的设计理论主要有容许应力法和极限状态法。目前铁路桥规采用容许应力法，公路桥规采用极限状态法。容许应力法的验算式表现为应力的形式，极限状态法的验算式表现为荷载效应的形式。墩台身一般按偏心受压构件验算。现仅简介铁路桥规（《铁路桥涵混凝土结构设计规范》TB10092—2017）的验算方法，公路桥规的验算方法见《公路圬工桥涵设计规范》（JTG D61—2005）。

（1）截面强度验算

验算截面通常选在墩台身的底面与截面突变处。当桥墩较高时，由于最不利截面不一定在墩底，需沿墩身每隔2～3m 选取一个验算截面。

容许应力法验算式为

式中　N——作用于墩台顶面处的轴向压力（MN）；

G——检算截面以上顺轴向的墩台自重（MN）；

A——检算截面的全面积（m2）；

Mx，My——对截面主轴的计算弯矩（MN·m）；

Ix，Iy——对截面主轴的惯性矩（m4）；

x，y——应力点至主轴的距离（m）；(www.xing528.com)

ηx，ηy——检算截面上弯矩 My和 Mx的增大系数，具体计算方式参见《铁路桥涵混凝土结构设计规范》（TB10092—2017）；

[σ]——中心及偏心受压容许应力（MPa），其值按桥规取用，若荷载组合中包含附加荷载，[σ] 值可适当提高。

如果由式（7.13）算得的σmin为负值，则说明截面的一部分已处于受拉状态，应视其退出工作。此时需按照只有部分截面承受压力的原则，重新确定受压区范围，以求最大压应力，也即进行应力重分布计算。

应力重分布计算根据三项基本条件进行，即平截面假定（截面应变按线性分布）、弹性体假定（应力、应变关系符合胡克定律，但受拉区不参加工作）、力的平衡条件。对于单向偏心受压的矩形截面，重分布以后的最大压应力如图7.42所示。

图7.42　矩形截面应力重分布

或

式中　b——截面宽度；

，称为应力重分布系数，它与外力的偏心率有关。

对于其他形状的截面，特别是各种截面在双向偏心（斜偏心）下受压的情况，验算较为繁杂但计算原理相同，通常可查用已有计算图表，或利用相应的计算机程序计算。

（2）截面合力偏心距验算

为防止圬工结构裂缝开展过大而影响耐久性，并保证结构有足够的稳定性，应进行本项验算。

容许应力法验算式为：

式中　[e0]——容许偏心距，按铁路桥规取用，一般有[e0]=α·y，　α=0.5～0.7，y 为截面形心至最大压应力边缘的距离。

其他符号意义同前。

（3）纵向挠曲稳定性验算

挠曲稳定性验算通常简化为常规的强度验算形式，而引入弯矩增大系数或弯曲系数。验算式为：

式中　ηx，ηy——弯矩My，Mx的增大系数，其值按规范相应公式计算。

（4）墩台顶弹性水平位移验算

对较高的墩台为保证其具有足够的刚度，应按下式验算墩台顶顺桥向或横桥向的弹性位移：

式中　L——相邻墩台间的最小跨径（m），铁路桥L ＜24m时仍以24m 计；

Δ——墩台帽顶面处的水平位移（mm），包括由于墩台身和基础的弹性变形，以及基底土不均匀沉降的影响。

墩台身的弹性变形引起的墩台顶水平位移，可把墩台身作为一固定在基础顶面的悬臂梁，不考虑上部结构对墩台顶位移的约束作用，可依材料力学或结构力学公式计算。基础变位引起的墩台顶水平位移应根据基础类型采用相应的计算方法确定。

重力式墩台的墩台帽一般可不进行验算，而按构造要求配筋。采用挑臂式墩台帽的重力式墩台，需要配置受力钢筋，挑臂部分按悬臂梁计算。