最小二乘拟合法在海洋潮汐与水位控制中的应用

最小二乘拟合法在时差法以潮时差为参数描述水位关系的基础上，增加了潮差比与基准面偏差等参数，并采用最小二乘拟合逼近技术求解参数，通过空间内插三个参数而实现水位的空间内插。

5.2.3.1　基本原理

设A、B两站的水位分别记为hA(t)与hB(t)，则两站同步水位之间的关系描述为

式中，γ为放大或收缩比例因子，定义为潮差比；δ为水平移动因子，定义为潮时差；ε为垂直移动因子，定义为基准面偏差。三者统称为潮汐比较参数。如图5.17所示。

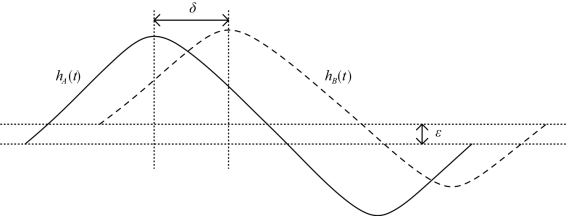
图5.17　最小二乘拟合法中的水位关系示意

结合图5.17，式(5.12)对两站水位关系的描述为:A站的水位曲线经平移(潮时差)、放大或缩小(潮差比)、垂直升降(基准面偏差)后与B站的水位曲线相同。因此，最小二乘拟合法必须满足的前提条件是两站水位曲线相似，与三角分区(带)法和时差法相同。

5.2.3.2　潮汐比较参数的求解

拟求解的潮汐比较参数组成未知参数向量

将式(5.12)按泰勒级数展开，得

式中，h′A(t＋δ0)为hA(t)在X0处对δ的偏导数。

按间接平差原理，将式(5.17)转为观测方程形式

设同步时段内n个时刻的水位，记为ti(i＝1，2，…，n)。每个时刻构建如式(5.18)的观测方程。根据间接平差的原理，观测方程组形式为

(www.xing528.com)

假设各观测互相独立，则观测值权阵可设为单位阵。按间接平差原理，求解得

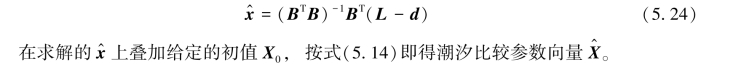
在应用上述原理求解两站间的潮汐比较参数时，需注意以下四点:

(1)计算过程中需要求解hA(t)在X0处对δ的偏导数以及在t＋δ0时刻的水位值，因此，需对观测水位序列拟合，以差分方式近似求解偏导数并内插出水位值。拟合内插的方法可参见附录B。

(3)前提条件是两站的水位曲线是相似的，与时差法、三角分区(带)法相同。

(4)两站间的潮汐比较参数不是固定值，需按测深时刻选取时段进行求解，如以测深时刻为中心的一天同步水位数据进行求解。

5.2.3.3　水位改正数的计算

对于任一测深点P，计算各站相对基准站的潮汐比较参数，将参数内插至该测深点处，其水位由基准站水位按测深时刻、相对于基准站的潮汐比较参数进行推算。潮汐比较参数的空间内插与时差法的原理一致，按两站带状模式与多站区域模式简述如下:

1.两站带状模式

若取A站为基准站，由两站同步水位按最小二乘拟合法原理求解出B站相对于A站的潮汐比较参数γAB、δAB和εAB。假设潮汐比较参数在两站间与距离成比例地均匀变化，参照图5.13与图5.14，按下式内插出P点相对于A站的潮汐比较参数。

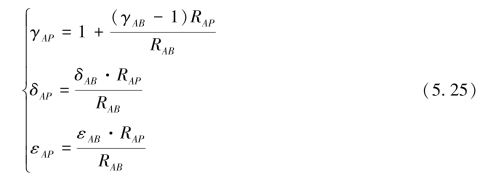
测深点P处在测深时刻t的水位改正数hP(t)为

2.多站区域模式

以不共线的3个验潮站为例，如图5.15所示，若取A站为基准站，由同步水位数据分别求解出B、C站相对于A站的潮汐比较参数。假设3个潮汐比较参数分别呈平面分布，参照图5.16以及式(5.8)至式(5.10)的原理分别内插出P点相对于A站的3个潮汐比较参数γAP、δAP与εAP，最后由式(5.26)计算水位改正数hP(t)。

在两站带状模式与多站区域模式中，最小二乘拟合法是将3个潮汐比较参数按直线或平面进行空间内插至任一测深点，因此，同时刻水位在整个测区空间上是连续分布的。