海洋潮汐与水位控制：时差法求解潮时差

时差法是利用相邻站的同步水位数据求解站间的潮时差，通过空间内插潮时差而实现水位的空间内插。其假设条件与三角分区(带)法相同:相邻两站之间的水位传播均匀，潮差和潮时的变化与距离成比例。

5.2.2.1　两站间潮时差的求解

求解两站间的潮时差是时差法的关键步骤，基本原理是将相邻两站的水位视为信号，运用数字信号处理技术中的互相关函数，求得两站间的潮时差。设A、B两站的水位分别记为hA(t)与hB(t)，同步时段内存在n个同时刻的水位，记为ti(i＝1，…，n)。两水位曲线的相似程度可由水位采样值序列的相关系数R来量化，由下式计算

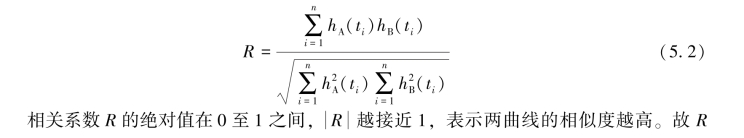
在应用上述原理求解两站间的潮时差时，需注意以下三点:

(1)两站的水位曲线是相似的，经过平移后的变化趋势应基本一致。这是时差法必须满足的前提条件，与三角分区(带)法相同。

(2)设水位观测的时间间隔为Δt，一般为5分钟、10分钟或1小时等，若直接由观测水位序列作为水位采样值hA(ti)与hB(ti)，则平移的最小间隔为Δt，求解潮时差的误差过大。因此，需对观测水位序列进行加密，可采用拟合内插的方法，参见附录B。

(3)水位是众多周期分潮以及非周期余水位的组合，因此，两站间的潮时差不是固定值，需按测深时刻选取时段进行求解，如以测深时刻为中心的一天同步水位数据进行求解。

5.2.2.2　两站带状模式

如图5.13所示，A与B为验潮站，两站间的直线距离为RAB；P为任一测深点，在两站连线上的垂足至两站的距离分别为RAP与RBP；测深时刻记为t。

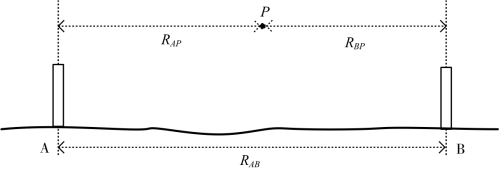
图5.13　两站带状模式示意

首先，取A站为基准站，由两站同步水位按时差法原理求解出B站相对于A站的潮时差τAB。因假设潮时在两站间与距离成比例地均匀变化，故可按距离线性内插出P点处相对A站的潮时差τAP:

其次，计算P点测深时刻t相对应的A站、B站同相时刻，设为tA、tB，按水位曲线间的潮时差关系，得

最后，假设P点、A站、B站的同相潮高hP(t)、hA(tA)、hB(tB)与距离成比例，如图5.14所示，以A站为基准构建坐标系，横轴为相对A站的距离R，纵轴为同相潮高h。

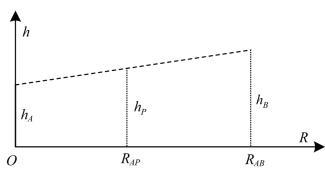
图5.14　同相潮高按距离线性内插

由图5.14易得

(www.xing528.com)

将式(5.5)代入式(5.6)，整理得测深点P的水位改正数hP(t):

时差法以潮时差描述水位在空间上的变化，而潮差的变化是通过式(5.7)的形式而顾及。

5.2.2.3　多站区域模式

以不共线的3个验潮站为例，如图5.15所示，A、B与C为验潮站，P为任一测深点，测深时刻记为t。

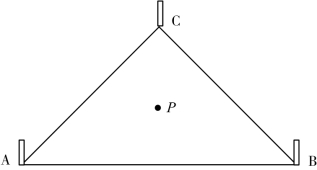
图5.15　三站区域模式示意

首先，取A站为基准站，由同步水位数据按时差法原理分别求解出B、C站相对于A站的潮时差τAB、τAC。因假设潮时在空间上均匀变化，故可假设潮时差呈平面分布。如图5.16所示，以A站为时差基准构建xyτ空间直角坐标系，三个验潮站处的坐标分别为A(xA，yA，0)、B(xB，yB，τAB)与C(xC，yC，τAC)，其中，x、y为其位置坐标。

图5.16　三站线性内插示意

这里将利用空间几何中过不共线三点确定平面方程的原理，简述如下。在xyz空间直角坐标系中过不共线三点(x1，y1，z1)、(x2，y2，z2)与(x3，y3，z3)的平面方程可设为

式中，a、b、c与d为方程的系数。将三点的坐标代入式(5.8)，可推导出系数为

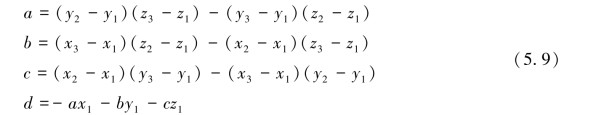
对于平面上的任一点P(xP，yP，zP)，若xP、yP已知，则由式(5.8)可得

将式(5.9)代入上式可得zP的解析表达式。

利用上述原理，由A、B、C三点坐标求解出所在平面的方程，进而求解出P点处相对于A站的潮时差τAP。

其次，计算P点测深时刻t相对应的A站、B站与C站同相时刻，设为tA、tB、tC，按水位曲线间的潮时差关系，得

最后，假设P点、A站、B站、C站的同相潮高hP(t)、hA(tA)、hB(tB)、hC(tC)呈平面分布，构建xyh空间直角坐标系，由A(xA，yA，hA)、B(xB，yB，hB)、C(xC，yC，hC)三点坐标求解出所在平面的方程，进而求解出P点处的水位改正数hP(t)。

在两站带状模式与多站区域模式中，时差法是将潮时差以及同相潮高都按直线或平面进行空间内插至任一测深点的测深时刻，因此，时差法的同时刻水位在整个测区空间上是连续分布的。这是时差法相对于三角分区(带)法的重要改进。