深度基准面传递：海洋潮汐与水位控制

由前述深度基准面的稳定性可知，由短期水位数据计算深度基准面L值的精度较低，通常应由邻近长期站传递确定。常用的传递方法有空间内插法、略最低低潮面比值法、潮差比法与差分订正法，下面介绍四种方法的数学模型、假设条件与使用方法。在表述中，统一将长期验潮站(基准站)记为A站，而将短期站(待传递站)记为B站。

4.3.3.1　空间内插法

空间内插法是指采用加权线性插值、多项式拟合、克里金等方法，由短期验潮站周边多站的L值内插出短期验潮站处的L值。以距离倒数加权插值法为例，简述其原理。

距离倒数加权插值法，也称为反距离加权插值法，是以距离倒数为权的加权线性插值方法。设传递时应用邻近n个验潮站，各站的L值为Li，短期站至各站的距离为Si，则短期站的L值由下式内插计算

该方法基于L值在区域呈线性分布的假设:①当n＝2时，距离取为短期站在两基准站连线上的垂足至基准站的距离，垂足应处于两基准站之间，且短期站至垂足的距离不能过大。②当n≥3时，取短期站至各站的距离，应保证短期站处于基准站网的内部。

空间插值法无需水位数据或调和常数等信息，因此，只能应用于L值变化线性且平缓的小范围海域，同时应尽量保证是内插的方式，避免外推。中国近海及邻近海域的深度基准面空间分布如图4.13与图4.14所示，单位为厘米(许军，等，2020)。

由图4.13与图4.14可看出，深度基准面L值在中国近海呈现复杂的非线性分布，因此应谨慎使用空间内插法，当存在同步水位数据或调和常数信息时，应尽量选择其他传递方法。

4.3.3.2　略最低低潮面比值法

略最低低潮面，又称印度大潮低潮面(Indian spring low water，ISLW)，是由英国潮汐学家达尔文(G.Darwin)考察印度洋潮汐时提出，定义为四个最大主分潮M2、S2、K1与O1的振幅和。

略最低低潮面计算简便，考虑了半日潮与日潮的作用，但未顾及迟角的影响，因此不能反映潮汐变化本身的复杂关系，特别是不能体现日潮不等的特征。实际工作表明，有的港口的很多低潮面落在该面之下(方国洪，等，1986)。在1957年前，中国部分海区的深度基准面采用略最低低潮面。

图4.13　深度基准面L值分布(一)

略最低低潮面比值法是假设略最低低潮面量值与深度基准面L值成线性比例关系:

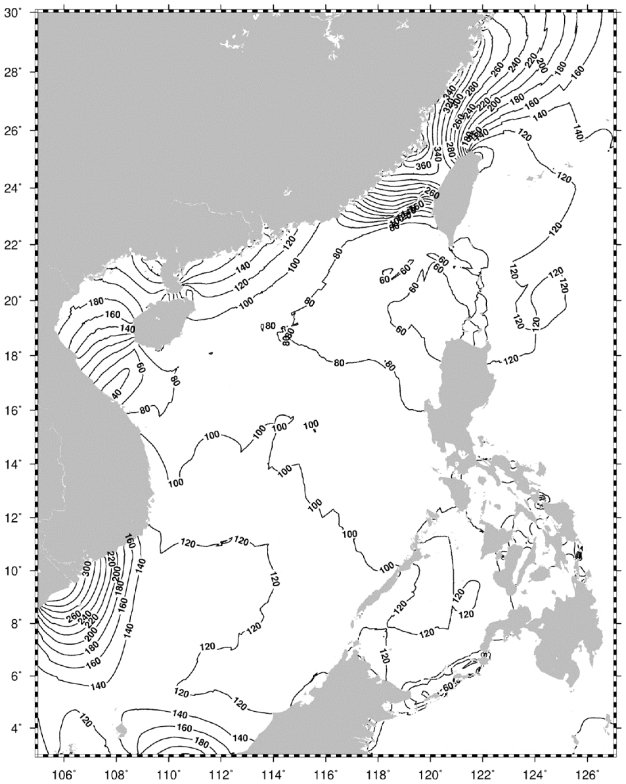
图4.14　深度基准面L值分布(二)

略最低低潮面比值法假设略最低低潮面与理论最低潮面的比值(后续简称比值)在相邻站处相等。因此，该方法的传递精度取决于比值的一致性。比值的空间变化越平缓、空间尺度越大，则适用性越好。利用精密潮汐模型(详见5.3小节)计算各网格点处的略最低低潮面，进而结合深度基准面模型(许军，等，2020)计算各网格点处的比值，比值的空间分布如图4.15与图4.16所示。

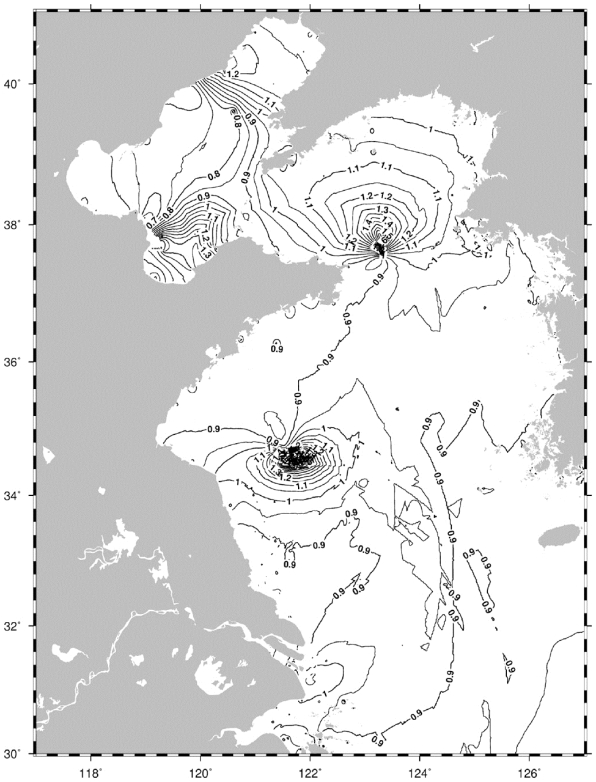
图4.15　比值的空间分布(一)

由图4.15与图4.16可看出，比值在空间上的复杂分布，使得传递误差在空间上并不是均匀分布的，适用性在空间上存在差异。因比值法的传递精度完全取决于站间比值的一致性，故不要求站间的潮汐类型相似，也不能以距离或潮汐类型相似性作为判断比值法适用性的标准，而图4.15和图4.16可作为判断的参考。

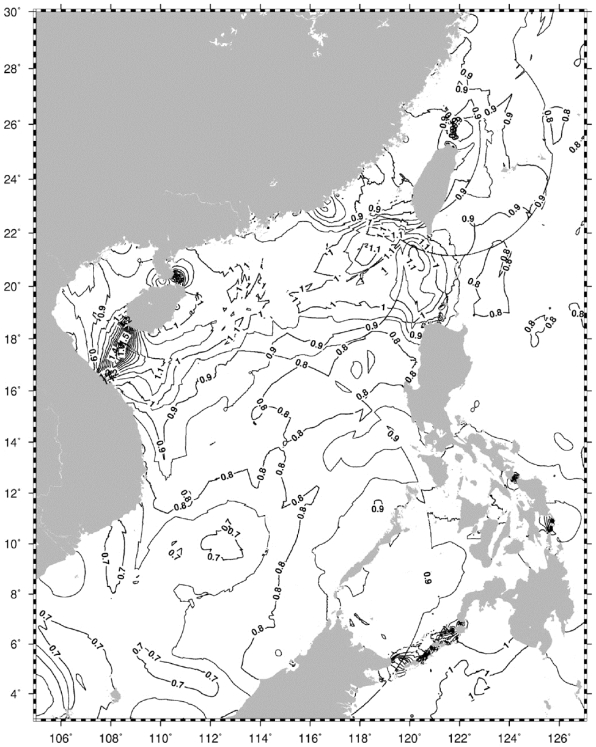
图4.16　比值的空间分布(二)

在实践应用中，短期站的略最低低潮面是由短期实测水位数据，经潮汐分析获得主要分潮调和常数后按式(4.43)计算的。潮汐分析的精度与水位数据时长有关，数据时长越短，调和常数的精度与稳定性越低，进而略最低低潮面以及传递精度也就越低。中国沿岸典型验潮站统计表明:随着同步时长的增大，传递误差的变化幅度在减小，同步时长达到7天时，传递误差可认为已较稳定(许军，等，2017)。

4.3.3.3　潮差比法

理论最低潮面是理论上可能的最低潮面，故潮差越大，L值应越大，潮差比法假设这种关系成线性比例关系，数学模型为(www.xing528.com)

式中，RA、RB分别为两站的潮差。因此，该方法需要两站同步水位资料确定潮差比。按潮差或潮差比的选取方式，潮差比的具体实现分为以下几种:

(1)潮差选取为平均潮差(mean range of tide，Mn)。

潮差为相邻的高潮和低潮之间的水位高度差，若设高潮位和低潮位分别为HW、LW，则潮差R为

平均潮差取为时段内所有潮差的平均值

式中，n为潮差的个数。

将式(4.46)代入式(4.47)，得

高潮位与低潮位的算术平均值分别称为平均高潮面(mean high water，MHW)与平均低潮面(mean low water，MLW)。平均潮差是时段内平均高潮面与平均低潮面的差值。

(2)潮差选取为平均大的潮差(great diurnal range，Gt)。

对于规则半日潮与规则日潮类型，日潮不等现象不明显，平均潮差代表了潮差的大小，此时平均潮差越大，其深度基准面越低，即L值越大。但对于不规则半日潮与不规则日潮等混合潮类型，日潮不等现象明显(考察图2.15)，部分或大部分日子内每天的两次高潮潮位间(低潮潮位间)存在明显的高度差，此时，平均潮差在一定程度上已失去了潮差大小的指标意义。

平均大的潮差定义为平均高高潮面与平均低低潮面的差值，其中，平均高高潮面(mean higher high water，MHHW)、平均低低潮面(mean lower low water，MLLW)分别为高高潮位与低低潮位的算术平均值。平均大的潮差为

对于日潮或不规则日潮类型，若每日只出现一次高潮与低潮时，唯一的高潮与低潮分别标识为高高潮与低低潮。由定义可知，平均大的潮差与深度基准面的最低潮意义更加符合。

(3)潮差比按最小二乘拟合法的数学模型计算，取为γ，计算方法见5.2.3小节。

上述三种选取方式的前提条件都是A、B两站的潮汐类型相似，判断依据除潮汐类型数相近外，水位变化曲线应相似，重点是日潮不等特征。在实践应用时，两站在日潮不等现象方面应保持一致，特别是每日的高潮与低潮的个数应基本一致，且高高潮、低高潮、高低潮与低低潮等特征潮位的出现顺序应一致。

由水位变化规律知，在(规则或不规则)半日潮类型的大潮期间与(规则或不规则)日潮类型的回归潮期间，潮差明显大于其他时段，这更符合于深度基准面作为极限低潮面的定义。因此，短期验潮站通常布设在大潮(回归潮)期间或包含大潮(回归潮)。利用大潮(回归潮)期间的平均潮差或平均大的潮差，由潮差比法传递确定深度基准面的精度将更高。大潮(回归潮)期间通常是指包含大潮(回归潮)的前后各一天，共计三天的时段。对于上述三种选取方式，是指只统计大潮(回归潮)期间的平均潮差或平均大的潮差、大潮(回归潮)期间同步水位由最小二乘拟合法计算的潮差比。

4.3.3.4　差分订正法

差分订正法是利用长期站的同步水位数据对短期站的调和常数实施差分订正，由订正后的调和常数计算理论最低潮面。步骤分为两步:

(1)由短期验潮站与其邻近长期站的同步水位数据，经潮汐分析分别获得两站同步期间的调和常数。由长期站的长期与同步期间的调和常数，对短期验潮站的调和常数实施差分订正。原理见3.6.3小节。

(2)利用长周期分潮空间分布尺度大的特点，直接引用长期站的长周期分潮调和常数，结合订正后的调和常数，按定义算法计算理论最低潮面。

差分订正法的关键在于第一步，因此，应用该方法需满足两个前提条件:

(1)数据条件:两站具有同步水位数据以及长期站的长期分析结果。通常要求同步时长能达到15天或以上，同步时长越长，订正的精度越高。

(2)调和常数差分订正的假设条件:两站的调和常数变化具有较强相关性和近似一致性。实践表明:相邻数十千米内的两站，若处于同一潮波系统，则一般是符合的。对于江河口等海域的站点，需要检测区域的适用性。