深度基准面在海洋潮汐与水位控制中的定义

深度基准面是海图图载水深的起算面，为了保障航行安全，深度基准面选为某种甚少能达到的低潮面，相应的图载水深是相对保守的水深，任意时刻的瞬时水深都甚少能小于图载水深。因此，深度基准面是一种潮汐基准面，深度基准面L值与潮差的大小有着密切的联系。确定的基本原则是:既要考虑到舰船航行的安全，又要照顾到航道的使用率。通常以“保证率”来表达这一原则。深度基准面的保证率是指高于深度基准面的低潮次数与低潮总次数之比。我国通常以95%为标准，国际海道测量组织要求水位很少会低于这个面，即在正常的天气情况下，水位都高于深度基准面，只有在特殊地点和遇特殊天气时水位才低于该面。

世界各沿海国家据潮汐性质的特点定义了多种深度基准面，甚至有些国家在其不同的海域采用了不同的定义。常用的定义有平均大潮低潮面、最低低潮面、平均低潮面、平均低低潮面、略最低低潮面、平均海面、最低天文潮面和理论最低潮面等，其中最低天文潮面是国际海道测量组织推荐的定义，而理论最低潮面是我国法定的深度基准面。

4.3.1.1　最低天文潮面

最低天文潮面(lowest astronomical tide，LAT)最初是由英国海军部提出的。其定义是，在平均气象条件下和在结合任何天文条件下，可以预报出的最低潮位值。同理，最高天文潮面(highest astronomical tide，HAT)定义为可以预报出的最高潮位值。1995年，国际海道测量组织推荐其会员国统一采用最低天文潮面为海图深度基准面。现在越来越多的国家开始采用最低天文潮面作为本国的深度基准面。

在算法具体实现上，可采用黄金分割法预报某个连续19年时段的高低潮潮位，分别取低潮中的最低潮位值(取正)和高潮中的最高潮位值作为最低天文潮面与最高天文潮面的量值。

4.3.1.2　理论最低潮面

理论最低潮面，也称为理论上可能最低潮面，旧称理论深度基准面、海图深度基准面。我国自1956年起，将深度基准面统一于理论最低潮面，采用弗拉基米尔斯基算法，由Sa、Ssa、Q1、O1、P1、K1、N2、M2、S2、K2、M4、MS4、M6等13个分潮叠加计算可能出现的最低潮位。

由26个变量的非线性函数，难以严密地推导出最小值。弗拉基米尔斯基算法采用理论化简的方法，其基本原理是依据分潮间的平衡潮理论关系引入近似假设，将多变量函数简化为K1分潮相角φK1的单变量函数，最后以适当间隔对φK1离散化，获得一组函数值，取最小值(符号为负)，则该值的绝对值即为相对于平均海面的理论上可能最低潮面。此处略去化简推导的过程，直接给出计算公式。13个分潮在理论上可能的最低潮面由下式表示:

式中，L8、Lshallow与Llong分别为8个天文分潮、3个浅水分潮与2个长周期分潮的贡献，具体分别为式(4.26)、式(4.27)与式(4.28)。

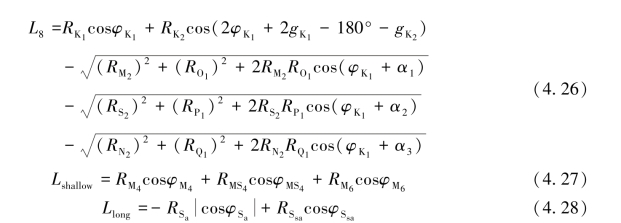
式(4.26)至式(4.28)中，R＝fH，H、g和f是下标所对应分潮的调和常数和交点因子，φK1为K1分潮的相角。其他变量由分潮的调和常数按下列式计算:

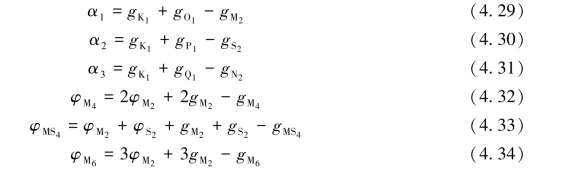
φM2的计算分为以下两种情况:

(1)当RM2≥RO1时

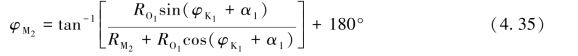(www.xing528.com)

(2)当RM2＜RO1时

φS2的计算分为以下两种情况:

(1)当RS2≥RP1时

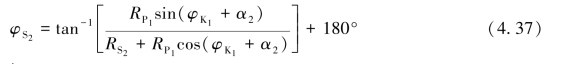
(2)当RS2＜RP1时

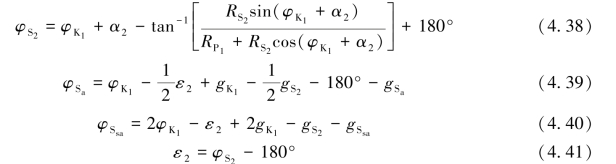
由13个分潮的调和常数及式(4.26)至式(4.41)，将式(4.25)简化为K1分潮相角φK1的单自变量函数。φK1从0°至360°变化以适当间隔离散取值，可求得L的最小值，其绝对值即为深度基准面L值。

上述式中交点因子f也是变量，依月球的升交点经度N而定，变化周期约为18.61年。在求式(4.25)的极值时，必须选择起作用相对大的f值，由表4.1查出。

表4.1　交点因子数值表

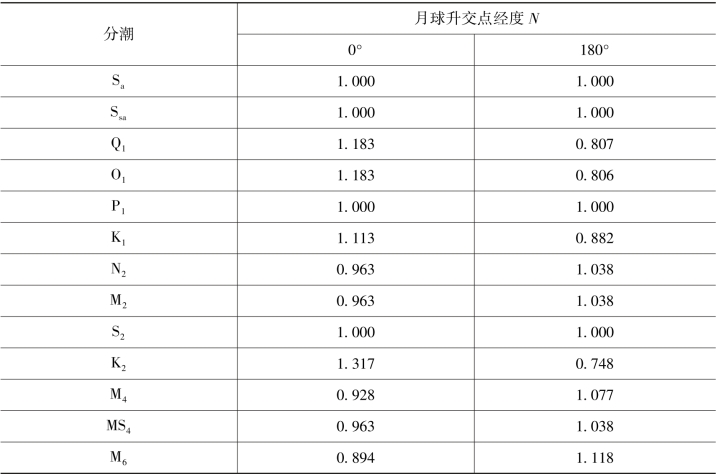
依潮汐类型由表4.1选取交点因子:

(1)规则日潮类型，交点因子选取N＝0°时的值；

(2)规则半日潮类型，交点因子选取N＝180°时的值；

(3)混合潮类型(不规则日潮与不规则半日潮类型)，交点因子分别选取N＝0°与N＝180°时的值，由式(4.25)计算两组结果，选取绝对值大者为结果。

在算法实现时，也可都按混合潮类型处理，即由式(4.25)计算两组结果，选取绝对值大者为结果。