平均海面传递-海洋潮汐与水位控制

在海道测量工程实践中，布设的验潮站通常只验潮数天至数月。由前述平均海面的稳定性可知，短期平均海面的变化幅度较大，因此，短期验潮站的平均海面应由邻近长期站传递确定。常用的传递方法有水准联测法、同步改正法与回归分析法，下面介绍三种方法的数学模型、假设条件与使用方法。在表述中，统一将长期验潮站(基准站)记为A站，而短期站(待传递站)记为B站；上标L与S分别表示长期平均海面与同步期的短期平均海面，平均海面的量值是指在该站水位零点上的垂直距离。

4.2.3.1　水准联测法

水准联测法，也称为几何水准法，基本原理是假定两站的长期平均海面位于同一等位面上，即两站长期平均海面的高程相等，或者说假定两站的海面地形数值相同。图4.7为A站处水准联测法相关的示意图，图中:水尺代表验潮设备；水准点的高程为HA；水准点相对于水位零点的高差为h0A；长期平均海面在水位零点上的垂直距离为MSLLA。

图4.7　水准联测法示意图

由图4.7中相关参数推导A站的长期平均海面的高程，即图中的海面地形ζA:

类似地可推导出B站的海面地形ζB:

水准联测法假设两站的海面地形相等，由上两式得

整理上式得B站的长期平均海面在其水位零点上的高度为

由上式知，传递确定B站的长期平均海面需以下已知条件:

(1)两站旁存在水准点且高程HA、HB已知。

对于布设于沿岸的长期或短期验潮站，按规范要求通常都联测布设数个水准点，分为主要水准点与工作水准点。

(2)两站水准点与水位零点的高差h0A、h0B已知。

对于长期站A站，h0A为已知值，提供给使用者。对于布设于沿岸的B站，按规范要求需测定工作水准点与水位零点间的高差，可采用等外水准或水面水准测定。若以水尺测量水位，则可由水尺以等外水准方式直接测定h0B。若以验潮仪测量水位，则可增设水尺，利用一时段内水尺与验潮仪的同步水位数据确定水尺零点与验潮仪水位零点的高差关系，进而推算确定工作水准点与验潮仪水位零点间的高差h0B。

由水准联测法的原理，分析传递误差:

(1)假设条件:两站的海面地形相等。

实践统计以及图4.2海面地形模型等值线分布表明，海面地形在中国沿岸每100km变化约5cm。因此，两站间距离越近，假设条件的符合程度将越高。

(2)h0A、h0B测定误差。

因工作水准点通常在验潮设备旁边，直接测定的精度高。

(3)HA、HB的误差。

验潮站所处的沿岸是地壳沉降相对明显的区域，不同年份的测量成果间可能存在数厘米、甚至数十厘米的差异。从不同起算点联测确定两站的水准点高程时，将存在起算成果年份不一致的问题。以水准联测方式直接测定两站水准点间的高差则可消除或减弱该误差，设测定B站水准点相对A站水准点的高差为hAB，则式(4.5)化为下式

4.2.3.2　同步改正法

同步改正法，也称为同步季节改正法、海面水准法，基本原理是假定同一时段内两站的短期平均海面与长期平均海面的差异(通常称为短期距平)相等。

假设两站短期距平相等，由上式得

整理上式得B站的长期平均海面在其水位零点上的高度MSLLB为

由上式知，传递确定B站的长期平均海面需已知两站同步期间的短期平均海面。

据同步改正法的原理，其主要误差源是两站同步期短期距平相等的假设条件。由前述平均海面的稳定性部分可知:平均海面变化(短期距平)呈现明显的年周期；相邻站间的变化呈现较强的一致性；随着同步时长的增加，平均海面的变化幅度减小，变化的一致性增加。从分潮的角度，这与Sa分潮的空间分布尺度有关。Sa分潮中来源于天文引潮力的部分很小，主要来源于太阳辐射等气候的周期性变化。这决定了Sa分潮具有空间分布尺度大的特点，即较大尺度范围内的Sa分潮保持基本一致。图4.8为Sa分潮振幅的等值线分布图，单位为厘米。

由图4.8可看出Sa分潮的振幅从北向南逐渐减小，振幅变化5cm对应于沿岸海域数百千米范围。这表明短期平均海面的变化幅度具有空间分布尺度大的特点。Sa分潮迟角决定了平均海面变化在时间上的一致性，如两站的迟角相近，则两站的平均海面在时间上基本同步达到最高或最低。一般情况下，迟角的空间分布是以迟角的等值线(也称为同潮时)来表示。这里将Sa分潮迟角转化为平均海面达到最高的月份，也就是月平均海面达到最高时的月份。原因是Sa分潮的周期刚好为一回归年，对于海域上某处而言，月平均海面达到最高的月在每一年都相同。转化方法简述如下:

图4.8　Sa分潮振幅等值线分布(www.xing528.com)

(1)Sa分潮的杜德逊编码为056.555，由式(2.19)知，天文相角即为太阳平经度h。h的周期为回归年，由式(2.22)知，每年1月1日的相角都约为280°。

(2)设Sa分潮的迟角为g，相角的月变化率约为30°，则m月的相角V(m)为

当相角为360°(0°)时，Sa分潮的潮高达到最高，据此可概算出月m

图4.9为以月平均海面达到最高时的月表示中国沿海Sa分潮迟角分布，重点关注于沿岸海域，南海海域因季节环流的作用而呈现复杂的变化，图中未细致标注。

图4.9　中国沿海Sa分潮迟角分布(数字为月份)

由图4.9可看出，月平均海面出现最高的月具有明显的规律性:渤海为7月，黄海、东海外海和台湾周边为8月，长江口附近和浙江沿岸为9月，福建和广东大部、海南和广西为10月。整体上从北向南逐渐推迟。若从巴士海峡东西方向上观察，则是从巴士海峡的8月向西逐渐推迟至北部湾的10月。

结合图4.8与图4.9可知，Sa分潮在中国沿海具有空间分布尺度大的特点，这是提出并实践应用同步改正法的基础。两站距离越近，同步时长越长，则两站短期距平的一致性越好。因月距平在每年的变化基本相同，故在无法获得邻近长期站水位数据时，可采用所属海区历史数据统计的月距平，称为平均海面季节改正数，作为精度要求不高时的平均海面改正值。如国家海洋信息中心编制出版的各年度《潮汐表》，以附表形式给出各海区12个月的平均海面季节改正值。

同步改正法是实践中最常用的平均海面传递方法，具有原理与计算简单、精度高的优点。中国沿岸典型验潮站统计表明:同步7天，同步改正法基本能保证传递的中误差与极值误差在±10cm内；而同步15天与同步30天的精度相当，能达到厘米级(许军，等，2014)。但同步改正法在使用时需关注两站水位的同步性，应保证时段的严密同步，特别是同步时长相对较短的时候。如短期站以水尺只观测了白天的水位或验潮仪中间因故障出现缺测等，两站应只采用同时刻的水位数据分别计算短期平均海面，否则会出现较大的误差。

4.2.3.3　回归分析法

回归分析法，也称为线性关系最小二乘拟合法，基本原理是假定两站的短期距平具有比例关系。设比例为k，则

将式(4.7)代入上式，得

上式中k未知，需进一步假设两站的长期平均海面之间为线性比例关系，比例系数仍为k，则有

上式中C为未知常数项。将上式代入式(4.13)，整理得短期平均海面之间的关系如下

对比式(4.14)与式(4.15)可知，此时两站的长期平均海面与短期平均海面具有相同的线性关系。

为了由式(4.13)求得，需由式(4.15)计算出k。若将整个同步期作为一个时段，计算两站同步期的短期平均海面与，则仅能由式(4.15)列出一个方程，无法求解出k与C。因此，通常将同步期按天分解，每天的日平均海面都列出如式(4.15)的方程，设存在n天的日平均海面序列，当n≥2时，基于间接平差原理可求解出k与C。步骤简述如下:

1.构建观测方程组

计算两站每天的日平均海面，设为与，其中i＝1，2，…，n。式(4.15)是估计k与C的观测方程，将每天的日平均海面代入式(4.15)得观测方程

n天的日平均海面序列构建观测方程组如下

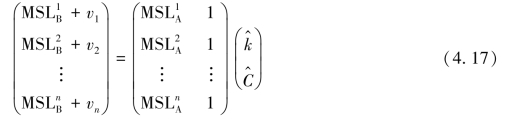
据间接平差的原理，观测方程组形式为

对照式(4.17)与式(4.18)，式(4.18)中相应矩阵的具体形式如下:

2.组建法方程及求解

假设各观测(每天的日平均海面)互相独立，则观测值权阵可设为单位阵。按间接平差原理，法方程为

由上式解得

理论上，只需同步两天即可由回归分析法传递确定短期站的长期平均海面。但由图4.3可看出日平均海面变化剧烈。中国沿岸典型验潮站统计表明:同步时长为3天时，其误差普遍较大，且部分时段的误差明显不合理。同步时长达到7天及以上时，其精度才与同步改正法相当，但部分站的极值误差仍相对偏大。因此，当同步时长在7天以内时，应谨慎使用回归分析法(许军，等，2014)。