海洋潮汐与水位控制：调和常数差分订正结果

在中期调和分析中，部分分潮间通过引入差比关系才实现了分离，差比关系是基于平衡潮的理论关系或者与邻近长期站关系一致的假设，求解存在着误差。另外，实测水位数据中还包含着余水位，对潮汐分析而言，余水位是扰动。水位数据时长越短，需引入的差比关系越多、余水位的扰动影响越大，这意味着潮汐分析的精度越低。潮汐分析实践表明:不同时段中期水位数据求解的调和常数存在明显的变化。以相距约70km的石臼所站与连云港站为例，以30天分段实施引入差比关系的中期调和分析，统计中期分析结果相对19年分析结果的差异，图3.10至图3.13分别为K1分潮与M2分潮的振幅差异和迟角差异，单位分别为厘米和度。

由图3.10至图3.13可看出，相比于长期分析结果，30天时长的分析结果存在明显的不稳定，分析精度较低。另一方面，这种不稳定在相邻的石臼所站与连云港站存在较强的相关性与近似一致性。经其他多站的统计，该规律普遍存在于中国沿岸。因此，孟昭旭等(2005)据此规律性提出利用差分原理由长期验潮站修正短期验潮站调和常数的方法，原理简述如下:某一短期站与其邻近长期站具有同步水位观测数据，对两站的同步时段水位数据分别实施中期调和分析。若长期站存在着长期分析结果，则可计算长期站的中期调和分析结果相对于长期分析结果的差异，比较对象不是各分潮的振幅与迟角，而是正弦分量和余弦分量。假设该差异在两站相等，将该差异订正至短期站的中期调和分析结果。

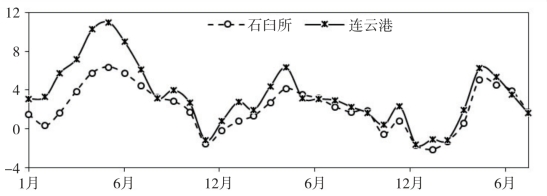
图3.10　30天时长K1分潮振幅变化

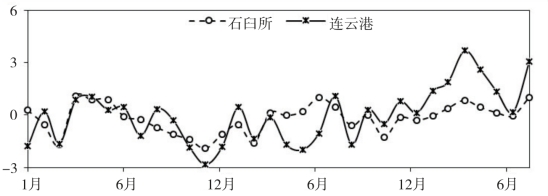
图3.11　30天时长K1分潮迟角变化

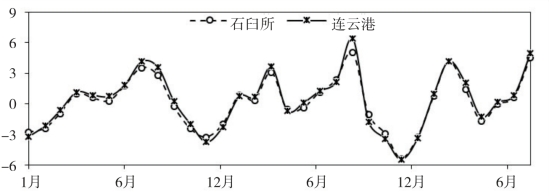
图3.12　30天时长M2分潮振幅变化

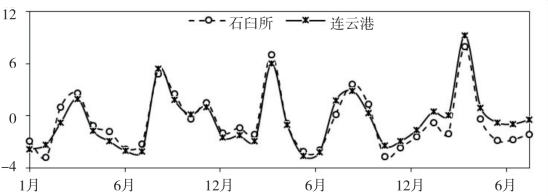(www.xing528.com)

图3.13　30天时长M2分潮迟角变化

设长期站与短期站分别为A站与B站，对于某一主分潮(其余分潮相同)，长期站A站的中期分析结果相对于长期分析结果的差异表示为

假设两站的差异相等，即下式成立

因此，B站经A站差分订正后的正弦分量与余弦分量为

由式(3.12)将订正后的正弦分量和余弦分量转换获得B站订正后的调和常数。

该方法的前提条件为两站在空间上相邻，具有同步的水位观测数据，长期站具有长期分析结果，且通常要求同步时长能达到15d或以上。两站在空间上越近，同步时长越长，则差分订正的精度越高。