前述基本天文参数与分潮相角的计算、调和分析最小二乘法的基本原理以及交点订正等原理与方法，结合最小二乘原理已可实现长期调和分析。这里给出基于间接平差原理的长期调和分析一般步骤，具有易于计算机编程实现、适用于任意时间间隔及数据间断等情况的优点。
1.分潮的选择
表3.6中的13个主要分潮是最常用、最重要的分潮，在此基础上可增加分潮以获取更加丰富的潮汐信息，如方国洪等(1986)给出的122个主要分潮，信息列于附录A的附表A.2。
2.水位观测数据整理
不同水位观测方法以及不同观测仪器获得的数据存储形式并无统一的规定。对于潮汐分析而言，所需的水位观测信息是每个观测的时刻t和该时刻水位在水位零点上的高度h(t)。因此，水位观测数据经各项必需的改正(如压力验潮仪观测数据的气压改正与水密度改正等)，都可转换为时刻t和水位高度h(t)序列的形式。需注意的是，水位高度的起算面必须是同一的水位零点。
3.构建观测方程组
长期调和分析的潮高模型为式(3.29)，是Hi与gi的非线性方程，将式中的余弦部分展开，得
式中，L为水位观测值向量；V为对应的误差向量；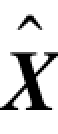
为未知参数向量；B为系数矩阵；d为常数向量，由式(3.44)知，d＝0。
若n个水位观测数据参与调和分析，则
选取了m个分潮，未知参数的个数为2m＋1，由式(3.44)可知未知参数向量为
(www.xing528.com)
对于每个观测时刻，可列出一个观测方程，对应于系数矩阵B的一行，行向量为
n个观测时刻的行向量组合成系数矩阵B。以任意时刻t为例，式(3.48)中相关量的计算步骤如下:
(1)按式(2.22)计算六个基本天文参数在t时刻的量值。在我国通常采用北京时(东8时区)系统，利用式(2.22)时可不实施时区转换，直接以北京时(东8区)代入计算，则调和分析求解的分潮迟角为北京时(东8区)的迟角。
(2)由各分潮的杜德逊数，按式(2.19)计算各分潮在t时刻的天文相角Vi(t)。
(3)由基本天文参数在t时刻的量值以及11个基本分潮的f、u计算式，计算11个基本分潮在t时刻的f、u。进而按附录A中的附表A.2中主要分潮与11个基本分潮f、u的推算关系计算各分潮在t时刻的f、u。
(4)将各量值代入式(3.48)，得观测时刻t对应的系数矩阵B的一个行向量。
(5)对n个观测时刻重复前面四步，得系数矩阵B。
4.组建法方程及求解
假设各观测互相独立，则观测值权阵可设为单位阵。按间接平差原理，法方程为
由上式解得
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
