交点订正-振幅乘系数和订正角公式

对于所选择的主要分潮而言，一年时长可以将它们相互分离。对于未选择的较小分潮，虽无须求取这些分潮的调和常数，但当较小分潮与主要分潮的会合周期长于一年时，对主要分潮调和常数的求解将产生扰动作用。由前述会合周期的概算可知，由一天、一个月、一年的水位数据分别可以相应地分辨不同族、不同群、不同亚群的分潮。一年时长不足以分辨同一亚群内的分潮，或者说，不能分离主要分潮和与其同一亚群内的小分潮。一年时长求解的主要分潮实际是该主要分潮所在亚群内所有分潮的综合结果。于是，为了尽量精确地分析出所需的主要分潮，将同一亚群内的分潮(角速率差别在量级上)进行合并，以亚群内最大分潮(即为主要分潮)的潮位表达为基础，分别在振幅和迟角上附加乘系数和改正量，以体现同一亚群内小分潮的贡献以及对最大分潮的扰动作用。振幅上的乘系数称为交点因子，记为f；迟角上的改正量称为交点订正角，记为u。此时，调和分析的潮高模型式(3.8)相应修改为

式中，f、u为各主要分潮的交点因子与交点订正角，代表了主要分潮所在亚群中小分潮的扰动作用，或者说，将亚群内所有分潮的作用通过f、u合并至主要分潮上。f、u随时间缓慢变化，f在1上下变化，u在0°上下变化。

以交点因子与交点订正角体现与表达同亚群小分潮扰动作用的订正方式称为交点订正，关键是计算各主要分潮在时刻t的交点因子f与交点订正角u。

3.5.1.1　理论严密计算方法

假设某个亚群内共存在N个分潮，则它们在时刻t的潮位之和(从平均海面起算)为

式(2.19)为天文相角计算式，将该式代入上式，并顾及各分潮属于同一亚群，即前三个杜德逊数相同，得

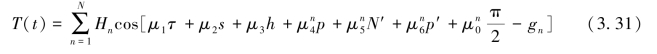
式中，μ1、μ2、μ3为该亚群中前三个相同的杜德逊数；上标或下标n表示量值属于第n个分潮。

对于同属于该亚群的N个分潮，分潮间的角速率差异非常小，实际海洋对分潮的响应可认为是十分接近的，从两方面理解:一是平衡潮展开的分潮振幅都远小于实际，但可认为各分潮的振幅增大比例是一致的，即实际分潮振幅间的比例关系与平衡潮的分潮振幅间的比例关系保持一致；二是分潮相角相对于平衡潮的天文相角都存在延迟，但可认为海洋对频率十分接近的分潮存在一致的影响，即分潮的迟角是一致的。因此，若该亚群N个分潮中第K个分潮最大，则各分潮的振幅与迟角可由第K个分潮的振幅与迟角表示为

式中，ρn为第n个分潮与第K个分潮的引潮力系数C之比，代表了平衡潮展开的两个分潮的振幅之比，即

进一步，将第n个分潮的杜德逊数以第K个分潮的杜德逊数表示，考虑到前三个杜德逊数相同，仅表示其他四个为

将式(3.32)与式(3.34)代入式(3.31)，得

为了将该亚群中N个分潮的潮位合并表达为一个分潮的形式，即

将式(3.37)代入式(3.35)，可将式(3.35)转换为式(3.36)。式(3.37)即为求解亚群中主要分潮交点因子f与交点订正角u的理论严密公式。

考虑到式(3.37)中上下两式的形式相似，可简化写为下式

以M2分潮为例，导出形如式(3.38)的f、u计算式。由附录A的附表A.1中提取M2分潮所在亚群的信息，列于表3.4(省去了前三个相同的杜德逊数:2，0，0)。该亚群共有5个分潮，其中第3个分潮为最大分潮，即M2分潮。(www.xing528.com)

表3.4　M2分潮所在的亚群合并

将表3.4中的相关量值代入式(3.38)，得

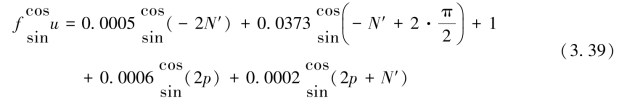
进一步化简为

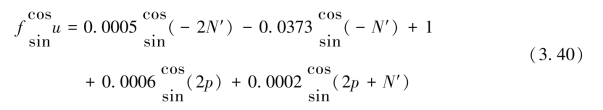
3.5.1.2　实用近似计算方法

对于每个主要分潮，都可由所在亚群的分潮信息推导出形如式(3.38)的f、u计算式。在实际应用中，常使用近似计算方法:按理论严密计算方法推导出M1、Mm、Mf、O1、P1、K1、J1、OO1、M2、L2、K2等11个分潮的如式(3.38)所示的计算式，而其他分潮的f、u由11个分潮的f、u推算出来，推算关系是基于引潮力展开理论推导得出的，误差很小。该11个分潮称为计算f、u的基本分潮。

11个基本分潮中，M1分潮的f、u计算相对特殊，达尔文为了分析方便以及错误使用了C值等原因，并不是以亚群中最大分潮为准进行合并，计算公式为

由式(3.41)计算所得的f不在1上下变化，而是在1.5上下变化；u不在0°上下变化，而是当p变化360°时，u也随着变化360°。达尔文对M1分潮的这种处理尽管存在一些缺陷，但对潮汐分析与预报的准确度并未造成影响，而如果重新导出f、u的计算式又会带来混乱，故式(3.41)一直被沿用下来。但应当注意的是，一般长期分析所得的各分潮振幅就是该分潮所在亚群最大分潮的振幅，唯独M1亚群最大分潮的振幅是计算所得M1分潮振幅的约1.42倍。(方国洪，等，1986)

除M1分潮外，其他10个基本分潮的f、u的计算式列于表3.5，表中前两列为相对主要分潮的杜德逊数差异Δμ4与Δμ5，后续每列对应于一个基本分潮的计算式。

表3.5　基本分潮的交点订正计算式

以Mm为例，表3.5中Mm所在列为其f、u的计算式，写成如式(3.38)的计算式

类似地，可由表3.5列出其他9个基本分潮的如式(3.38)的f、u计算式。

其他主要分潮的f、u采用11个基本分潮的f、u进行计算，表3.6为常用的13个主要分潮的f、u信息。

表3.6　常用的13个主要分潮信息

续表

以表3.6中的M4分潮为例，其f为M2的平方，而u为M2的2倍。