海洋潮汐与水位控制：引潮力的展开与分潮概念

2.4.2.1　展开的目的与基本过程

月球与太阳产生的引潮力是海洋潮汐的源动力，引潮力随着地球自转和地、月、日之间相对距离与位置等的变化而变化，这些天体运动呈现周期性质，决定了潮汐现象的周期性。在平衡潮理论假定的理想状态下，引潮力使海面升降以使海面在任意时刻都保持平衡状态，因此，海面升降的周期性规律可通过对引潮力的周期性分析而获得。引潮力作为保守力，也可通过对引潮势的周期性分析而实现。

在诸多海洋潮汐理论文献中，引潮力(势)的展开按研究对象可分为引潮力Ft(分为水平分量与垂直分量)、引潮势Ω、平衡潮Ω/g的展开。但从应用理解角度，展开的最终目标可认为是一致的:从理论上严密获取引潮力(势)的频谱结构，即展开为众多频率振动的叠加。若每个固定频率振动以余弦(或正弦，这里以余弦为例)Hcosσt形式表示，引潮力(势)统一以Θ表示，则目标是将Θ展开为下式的形式

式中，n表示振动数；H为振幅；σ为振动的角速率；t为时间变量。

每一固定频率的振动项被称为调和项或分潮，而这样的展开称为调和展开。因引潮力(势)取决于月球、太阳相对地球的运动，故展开的进程受限于太阳运动与月球运动的理论和数据，可分为以下几个主要阶段:

(1)第一展开式(拉普拉斯(Laplace)展开)。以P点和引潮天体的赤纬、天体时角为变量，对引潮力(势)进行展开，只简单分离出长周期、全日周期和半日周期三部分。

(2)第二展开式。以月地距离、月球在白道的真经度、平太阳时角、平太阳经度、白赤道交角、白赤道交点在赤道和白道的经度等为变量对引潮力(势)进行展开，但部分变量的变化范围达不到360°。

(3)第三展开式(达尔文(Darwin)展开)。达尔文于1883年以月球在白道的真实经度、平太阳经度、白赤交点的赤经和白赤交点在白道的经度等为变量对引潮力进行调和展开，每个展开项即为一个分潮，并对主要半日分潮和全日分潮进行了命名，这种命名一直沿用至今。但达尔文所得分潮振幅仍与时间有关，相角部分也不是随时间匀速变化，所以达尔文展开实质上并不是调和的，但是已经很接近调和项了。

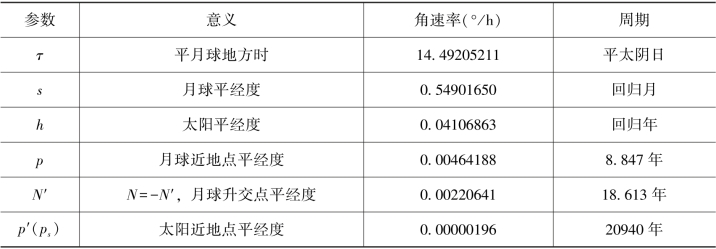
(4)第四展开式(杜德逊(Doodson)展开)。杜德逊采用布朗(Brown)月理(月球轨道有关参数的纯调和展开式)于1921年首次给出纯调和展开式，变量采用六个基本天文参数，列于表2.1。

表2.1　六个基本天文参数

式中，μ0是为了将调和项都化为余弦形式；μ0，μ1，…，μ6这7个系数都为整数。

因此，只要据式(2.19)计算出在t时刻的六个基本天文参数，便可由上式得知该分潮在t时刻的相角V。而该分潮的角速率σ是相角V对时间的导数，由式(2.19)对时间求导数，可由μ1，μ2，…，μ6与六个天文参数的角速率(表2.1)按下式计算角速率σ:

由上述可知，μ1，μ2，…，μ6确定了分潮的相角与角速率，故可作为识别区分不同分潮的标识，称为杜德逊数(Doodson number)。其中，μ1总为非负整数，而μ2，μ3，…，μ6在±12内，绝大多数取值在±4内。杜德逊设计“NNN.NNN”形式编码记录μ1，μ2，…，μ6，称为幅角数或杜德逊编码。N都为0至9的整数，第一个N直接取为μ1，而后续5个N为对应系数加上5。如某分潮的μ1，μ2，…，μ6分别为2，－2，2，0，0，0，则对应的杜德逊编码为237.555。对于极少数≥5和≤－5者，对应的N将以字母代替:L表示－1，X表示10，E表示11。至此，每个分潮都以μ1，μ2，…，μ6或杜德逊编码来唯一标识。

2.4.2.3　分潮的分群

由表2.1知，六个基本天文参数的周期相差很大，而μ1，μ2，…，μ6都是一些小的整数，因此在频谱图上，分潮的分布不是均匀的，而是一丛一丛的，通常将分潮按族、群和亚群来划分。首先按μ1＝0，1，2，3分成四个大的丛，叫做潮族0，1，2，3，即第一个杜德逊数相同的分潮处于同一潮族。

(1)属于潮族0的分潮，其周期长，故称为长周期分潮，而潮族0也称为长周期分潮族；

(2)属于潮族1的分潮，其周期约一天，故称为全日分潮，而潮族1也称为日周期分潮族；

(3)属于潮族2的分潮，其周期约半天，故称为半日分潮，而潮族2也称为半日周期分潮族；

(4)属于潮族3的分潮，其周期约1/3天，故称为1/3日分潮，而潮族3也称为1/3日周期分潮族。

在同一潮族中，又可按μ2的不同而分成更小的丛，每一丛叫做群，即前两个杜德逊数都相同的分潮处于同一群。在同一群中，可进一步按μ3的不同而分成若干个亚群，即前三个杜德逊数都相同的分潮处于同一亚群。

2.4.2.4　分潮的命名

杜德逊编码可唯一标识分潮，但在数百或数千分潮中，大部分分潮的振幅都很小。达尔文曾经对一些主要的分潮进行了命名，基本规则是以下标来表示分潮周期的大体长度:a，sa，m，f分别代表周期约为一年(annual)、半年(semi-annual)、一月(monthly)和半月(fortnightly)；而1，2，3分别代表周期约为一天、半天与1/3天。该命名规则一直沿用至今。

对于特别重要的分潮，根据其来源还有专门名称。月球和太阳引潮力中最主要的半日分潮分别为M2与S2，称为主要太阴半日分潮和主要太阳半日分潮，S2略小于M2的一半。由于月地距离变化而产生的主要半日分潮是N2，称为主要太阴椭率半日分潮，略小于M2的1/5。由于白道对赤道存在倾角，在月球引潮力中存在半日分潮K2；而因黄道倾角，在太阳引潮力中也存在半日分潮K2，两者角速率相同，合成的分潮K2，称为太阴太阳合成半日分潮，略大于M2的1/10。

由于白道倾角，在月球引潮力中存在两个大小基本相同的分潮O1与K1；而黄道倾角也造成两个大小基本相同的分潮P1与K1；两个K1分潮的角速率相同，合成的分潮K1称为太阴太阳合成全日分潮；而O1与P1分别称为主要太阴全日分潮与主要太阳全日分潮，O1略大于K1的2/3，P1略小于K1的1/3。月地距离变化造成的全日分潮主要有Q1、J1与M1，其中Q1最大，略小于O1的1/5，称为主要太阴椭率全日分潮。

附录A中的附表A.1列出了杜德逊展开获得的300多个分潮的信息，表中相对较大的分潮采用达尔文的分潮命名。

2.4.2.5　分潮相角与基本天文参数计算

分潮在时刻t的相角V(t)可直接按式(2.19)计算，或者选定某一时刻t0为起点(参考时刻)，按式(2.19)计算得出该时刻相角V(t0)。设从t0至t的时间间隔为Δt，则

式中，σ为分潮的角速率，通过式(2.20)计算。

在式(2.19)中，μ1，μ2，…，μ6对于某分潮而言是已知常数，故分潮相角的计算将归结于六个基本天文参数的量值计算。六个基本天文参数在时刻t的值由下式计算(www.xing528.com)

上式的相关说明如下:

(1)τ的计算依托于后续五个参数。后五式的右侧第一项为常数项，是1900年1月1日格林威治0时的量值，即上式是以该时刻作为参考历元。因此，时刻t应是世界时(格林威治0时区)，其他时间系统可按式(2.1)进行转换。设时刻t对应的世界时表示为Year－Month－Date Hour:Minu:Sec。

(2)后五式的右侧第二项的数值是指年变化率，IY是指从1900年开始累积的年数，即IY＝Year－1900，该项计算了累积年变化部分。

表2.2　累积日期序数计算表

续表

以计算M2分潮(杜德逊编码为255.555，μ0为0)2015年7月1日(东8区北京时)的24个整点时刻的相角为例，总结基本天文参数与分潮相角的计算方法与过程。该算例采用两种方法:一是按式(2.22)计算24个整点时刻的基本天文参数，再由式(2.19)分别计算对应的24个时刻的相角；二是按式(2.22)计算0时的基本天文参数，再由式(2.19)计算0时的相角以及由式(2.20)计算分潮角速率，最后由式(2.21)计算后续23个整点时刻的相角。方法一适用于计算任意时刻的分潮相角，对于本算例，将重复24次同一计算过程；而方法二虽略比方法一复杂，但在计算大批量固定时间间隔的分潮相角时，将具有更高的效率。下面演示方法二计算本算例的过程。

计算0时基本天文参数的过程如下:

1)时区转换

东8区北京时:2015-07-01 00:00

对应于世界时:2015-06-30 16:00

2)计算式(2.22)中的时间变量

3)按式(2.22)计算基本天文参数

计算24个整点时刻M2分潮相角的过程如下:

1)分潮信息

M2分潮:杜德逊编码255.555

对应杜德逊数2，0，0，0，0，0

μ0＝0

2)按式(2.19)计算0时相角

将0时(北京时)的基本天文参数值与分潮信息代入式(2.19)，得

3)按式(2.20)计算角速率

将表2.1的基本天文参数的角速率与分潮杜德逊数代入式(2.20)，得

4)按式(2.21)计算后续23个整点时刻的相角

将0时(北京时)的相角与分潮角速率代入式(2.21)，得