潮汐现象解释及海洋水位控制

因月球引潮力是太阳引潮力的2.17倍，故潮汐现象与月球的运动最密切相关。

2.4.1.1　月中天与高潮

地球上大部分海域在一天内会出现两次高潮(低潮)，这与月中天有关。月球经过该地的子午圈时刻，称为当地月中天(或太阴中天)，月球每天经过子午圈两次，离天顶较近的一次称为月上中天，离天顶较远的一次称为月下中天。图2.9为月中天时地球子午圈剖面上引潮力示意图，A、B在月球中心与地心O的连线上，此时A处为月上中天，B处为月下中天。

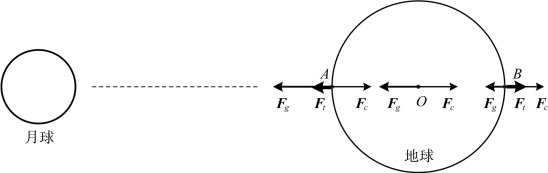
图2.9　月中天时引潮力示意

在图2.9中的A、O、B处，公转离心力Fc相同，月球引力Fg随着与月球距离的增大而量值沿A、O、B逐渐减小。其中，在A处，月球引力Fg的量值大于公转离心力Fc，引潮力Ft指向月球；在地心O处，两者的量值相等，引潮力为零；在B处，月球引力Fg的量值小于公转离心力Fc，引潮力Ft背向月球。按此思路可相应地推测地球上各点处的引潮力方向，海水在引潮力作用下流动并达到平衡状态，如图2.10所示。图中实线为地球未受引潮力时的等深海面，而虚线为月中天时，瞬时响应引潮力作用后的海面形态示意。

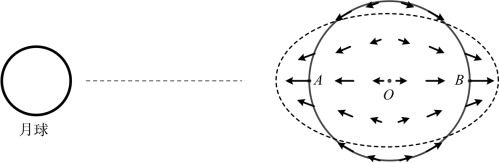
图2.10　月中天时引潮力及瞬时海面形态示意

由图2.10知，月上中天的A处与月下中天的B处引潮力的水平分量都为零，但其他处海水在引潮力“牵引”作用下向A处与B处堆积，因此A处与B处都出现高潮，而垂直于地月连线处出现低潮。由前述月球的运动可知，月上(下)中天的周期为一太阴日，比太阳日长50分钟，即为24小时50分钟。在一太阴日内，A处与B处将各经过一次月上中天、一次月下中天，因此每个太阴日内出现两次高潮。同理在每个太阴日内出现两次低潮。且易知，以平太阳时记，每天的高潮(低潮)比前一天的高潮(低潮)迟约50分钟。

2.4.1.2　月相与大潮、小潮

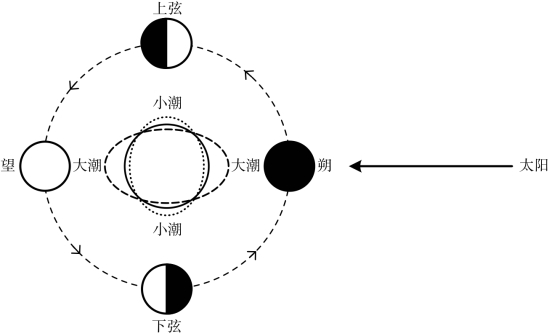
由前述图2.2知，潮差是逐日变化的。我国古代劳动人民早就发现潮差变化与月相变化(农历)相关。在朔(初一)望(十五、十六)达到半个月中的潮差最大，称为大潮；而在上弦(初七、初八)和下弦(廿二、廿三)达到潮差最小，称为小潮。图2.11为月相与大小潮示意图，图中实线为地球未受引潮力时的等深海面，虚线与点线分别为朔望、上下弦时瞬时响应月球引潮力作用后的海面形态示意。

如图2.11所示，当朔望时，太阳、月球、地球成一直线，月球引潮力作用与太阳引潮力作用叠加增强，此时发生大潮；而在上弦与下弦时，太阳、地球、月球成直角，月球引潮力作用与太阳引潮力作用的相互削弱最为显著，此时发生小潮。月相从朔开始经过上弦、望、下弦再回到朔的时间长度为一个朔望月。

2.4.1.3　月球赤纬与日潮不等、回归潮、分点潮、潮汐类型

月球的运行轨道(白道)与地球的赤道并不在同一平面内，相对于赤道面，月球在一回归月中两次经过赤道，各一次到达最南与最北。若在赤道坐标系中表示月球的位置，则月球在一回归月中两次赤纬为0，各一次赤纬达到南最大与北最大。因地球上各点所受的月球引力指向于月球，故易知月球赤纬不同时，引潮力以及海面形态也将不同。图2.12为月球分别经过赤道与达到最北时海面形态示意图。

当月球经过赤道时，图中A、B、C处为月上中天，出现高潮，经过半个太阴日(12小时25分钟)后为月下中天(即图中A′、B′、C′)，再次出现高潮，而且因引潮力一致而两次高潮的高度相等，此时的潮汐叫分点潮。

(www.xing528.com)

图2.11　月相与大小潮示意

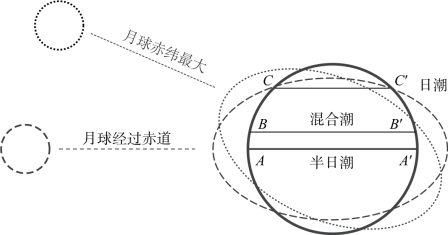
图2.12　月球赤纬变化时海面形态示意

当月球赤纬最大时，月上中天与月下中天的引潮力不一致，两次高潮的高度不相等，相应地两次低潮的高度也不相等。此种一日两次高潮(低潮)高度不等现象，叫日潮不等。日潮不等主要是由月球赤纬不为零引起的，当月球在最北或最南附近时，所产生的日潮不等现象最显著，此时的潮汐叫回归潮。分点潮与回归潮是月球赤纬变化而引起的，所以称为回归不等，其周期为半个回归月。

日潮不等现象还与地理纬度有关，如图2.12中A、B、C处:①A点处一个月内每天都有两次高潮或低潮，随着月球赤纬增大，日潮不等也相应增大，该类型变化规律的潮汐称为(规则或正规)半日潮类型；②B处虽一太阴日内也出现两次高潮或低潮，但日潮不等现象比A处显著，两相邻的高潮(低潮)的高度差十分明显，该类型变化规律的潮汐称为混合潮类型；通常可进一步细分为两种类型:一是每天都出现两次高潮或低潮，称为不规则半日潮(混合潮)类型；二是在回归潮前后数天每天将只出现一次高潮或低潮，称为不规则日潮(混合潮)类型；③C处，当月球经过赤道时，一太阴日内出现两次高潮和低潮，但潮差很小，可能完全消失；而当月球赤纬增大时，两个小的潮高(高低潮和低高潮)完全消失，每天只出现一次高潮与低潮，而且每天只出现一次高潮与低潮的日子在一个月内占大多数，该类型变化规律的潮汐称为(规则或正规)日潮类型。

2.4.1.4　月地距离与视差不等

天体与地球的距离可采用地平视差来表示。如图2.13所示，地球的平均半径为R，地心与天体中心的距离为r，通过天体中心作地球的切线，和地心与天体中心连线的夹角φ即为地平视差。

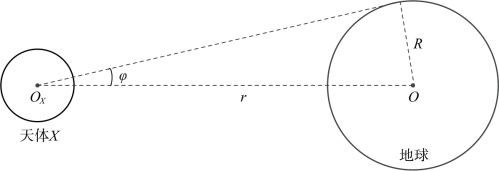
图2.13　地平视差

由图2.13易得

式中，R通常取赤道半径，即等于6 378km。由于φ很小，sinφ近似等于φ的弧度值。从而地平视差与天体至地心的距离成反比，因此，地平视差的大小可作为天体与地球间距离的指标参数。经计算，太阳的平均地平视差为8.794″，月球的平均地平视差为57′02.70″。月球绕地球、地球绕太阳的轨道都为椭圆，如图2.14所示。

图2.14　太阳、地球、月球距离变化

在一个月内，地月距离变化约50 000km，月球处于近地点时(图中M1)引潮力最大，太阴潮潮差相应地比其他时刻大；而处于远地点时(图中M2)的引潮力最小，太阴潮潮差相应地比其他时刻小。在一年内，日地距离也不同，地球处于近日点时(图中E1，每年1月2日前后)，太阳潮潮差增大；而地球处于远日点时(图中E2，每年7月2日前后)，太阳潮潮差减小。总之，潮差的大小还随月地距离与日地距离的大小而变化，因天文上以地平视差表示天体与地球的距离，故此种潮差不等现象称为视差不等。