改进的Clark模型--水文学原理（第2版）

上节所述Clark模型应用面积-时间曲线作第一次调蓄计算时，由于各等流时面积上的净雨输入相等，故属于集总模型。若需要考虑流域内净雨空间分布不均匀对汇流的影响，则可将每个等流时面积作为一个单元，分别采用各自的净雨进行汇流计算，即各单元的净雨不同，就构成简单的线性分布式流域汇流模型，其概念如图10.17所示。

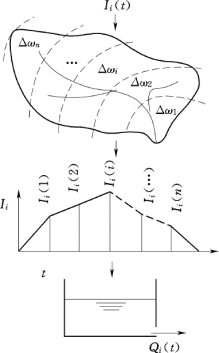
图10.17　改进的Clark模型示意图

设各等流时面积分别为a1，a2，…，ai，…，an，计算时段长为相邻两等流时线的时距。当流域内降雨空间分布不均匀时，Δt时段内各单元面积上的净雨量并不一定相等。设第j时段各单元面积上，即各等流时面积上的净雨量分别为I1j，I2j，…，Iij，…，Inj，这里I的第一个下角标表示单元序号，第二个下角标表示净雨时段序号。按照等流时线的概念，由第j时段净雨所形成进入线性水库的流量过程应为(www.xing528.com)

这一流量过程通过单一线性水库再进行一次调节计算，得到第j时段净雨形成的流域出口断面流量过程Qj（t）。若净雨有m个时段，可依次由上式得出Q1（t），Q2（t），…，Qj（t），…，Qm（t）。根据线性系统可叠加性，流域出口断面的总流量过程Q（t）应为各个时段净雨所形成的流量过程之和，即

改进的克拉克（Clark）模型通过按等流时面积划分单元面积而考虑了净雨的空间变化，但流域的调蓄作用仍是集总的，未能考虑各单元面积调蓄作用的差异。