当单系统的输入为单位脉冲函数δ时,系统所形成的输出称为脉冲响应函数。对于流域汇流系统,当输入为单位脉冲净雨时,所形成的输出则称为流域瞬时单位线(Instantaneous Unit Hydrograph,IUH)。所谓单位脉冲净雨指在流域上分布均匀,历时趋于零且强度趋于无穷大,而净雨量(净雨强度乘以净雨历时)为1个单位的输入过程。依据水量平衡原理可知,流域瞬时单位线的总面积等于1个单位。
将上述δ函数的定义代入式(10.23)就得到流域瞬时单位线的数学表达式:

式中:u(0,t)为流域瞬时单位线。
当上式中的系数am(m=1,2,…,M)和bn(n=1,2,…,N)均为常数时,所描述的流域汇流系统为线性时不变系统。若初始条件为零,式(10.27)的Laplace变换为
![]()
式中:A(P)/B(P)为系统的传递函数,而A(P)、B(P)分别为
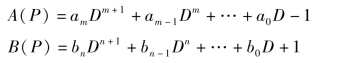
由于L[δ(t)]=1,所以

再取式(10.29)的拉普拉斯逆变换,可得
![]()
由此可知,流域瞬时单位线就是流域汇流系统传递函数的拉普拉斯逆变换。于是,流域瞬时单位线也称为流域瞬时响应函数或核函数。
对于线性时不变系统,取零为初始条件,式(10.23)的拉普拉斯变换为
![]()
将式(10.29)代入式(10.31),得到
![]()
而式(10.32)的拉普拉斯逆变换为
![]()
式(10.23)就是线性时不变系统在零初始条件下的解,又称为卷积公式。因卷积具有可交换性,式(10.33)也可写为
![]()
从式(10.34)推导可知,如果流域汇流系统为线性时不变系统时,若流域瞬时单位线已知,即可由净雨过程求得出口断面的径流过程线。式(10.33)或式(10.34)描述了流域上均匀分布净雨所形成的t时刻出口断面流量Q(t),物理概念如图10.10所示。
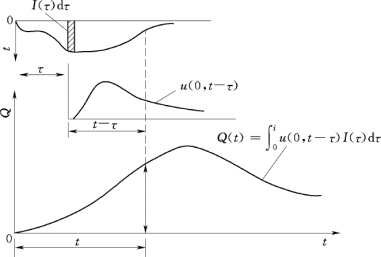
图10.10 卷积公式的物理概念
对比式(10.7)与式(10.34)可知

式(10.35)表明,流域瞬时单位线是汇流面积随时间的变化率,即汇流面积是由散布于流域各处,具有不同运动速度但能同时流达出口断面的净雨质点组成的。再对比式(10.20)与式(10.34),则有
![]()
式(10.36)表明,在流域内各处净雨质点汇流速度相同的特例中,流域瞬时单位线为面积-时间曲线。可见,流域瞬时单位线主要取决于流域地貌结构和净雨质点的汇流条件。
目前应用广泛的流域瞬时单位线是Nash模型[3],它将流域对洪水的调蓄作用设想为n个调蓄功能相同的串联水库,且每一水库的蓄水量s与出流量Q均为线性关系,其数学方程为

式中:Г(n)=(n-1)!,为n的伽玛函数;其余符号意义同第8章。
由式(10.37)可看出,瞬时单位线的形状取决于参数n、K,它们反映了流域的调蓄特征。参数n、K值一般由瞬时单位线的矩来确定,而矩又与净雨和流量过程线有关。参照图10.11,依据式(10.38)和式(10.39)可分别计算出净雨和流量过程的一阶原点矩和二阶中心矩:
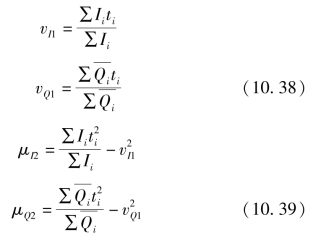
 (https://www.xing528.com)
(https://www.xing528.com)
图10.11 计算净雨和流量过程线
式中:vI1、vQ1分别为净雨、流量过程的一阶原点矩;μI2、μQ2分别为净雨、流量过程的二阶中心矩。
瞬时单位线的一阶原点矩v1和二阶中心矩μ2则为
![]()
而参数n、K与一阶原点矩和二阶中心矩的关系为
![]()
由净雨和流量过程推求瞬时单位线参数n、K的步骤可参阅下述例10.2。
【例10.2】 求例10.1中净雨和实测流量过程的瞬时单位线参数n、K值,Δt仍取6h。
解:计算步骤如下:
(1)依据式(10.38)和式(10.39)计算净雨过程的一阶原点矩vI1和二阶中心矩μI2,参阅表10.3;
vI1=201/53=3.79;μI2=981/53-3.792=18.51-14.36=4.15。
(2)依据式(10.38)和式(10.39)计算地表径流过程的一阶原点矩vQ1和二阶中心矩μQ2,参阅表10.4;
vQ1=41241/2025=20.37;μQ2=1130841/2025-20.372=558.44-414.94=143.50。
(3)计算瞬时单位线参数n、K:
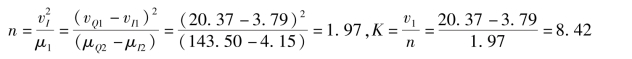
当n、K确定后,瞬时单位线方程就唯一确定了。
表10.3 净雨一阶原点矩和二阶中心矩计算表

表10.4 流量一阶原点矩和二阶中心矩计算表

瞬时单位线的净雨历时趋于零,故在实际汇流计算中需要应用S曲线将其转换为某一历时的时段单位线。流域瞬时单位线的S曲线可看作雨强为1个单位的连续净雨所形成的流量过程线,即瞬时单位线的积分曲线;其数学方程为

S曲线已由有关部门依据n,K制成表格,供查算使用,各类水文学教材中也均附有此表。
将瞬时单位线转换为Δt的时段单位线,需要应用u(Δt,t)=S(t)-S(t-Δt),其中u(Δt,t)为时段长Δt的无因次单位线。注意到瞬时单位线的面积为1,即
![]()
对于流域面积为Akm2,净雨为10mm,时段长为Δt,具有因次的单位线,可用下式计算:
![]()
式中:q(Δt,t)为Δt时段单位线的纵坐标,m3/s。
【例10.3】 应用例10.2的结果,n=1.97,K=8.42,求Δt=6h的时段单位线。
解:列表计算如表10.5,具体步骤如下:
(1)由n,t/K查S曲线表,填入表中③栏;再将此系列错后一行填入④栏;
(2)由第2行起,⑤=③-④,是Δt=6h时段单位线的相对纵坐标;
(3)⑥=[10A/3.6Δt]×⑤=[10×820/(3.6×6)]×⑤=379.6×⑤,就是Δt=6h,净雨为的10mm的时段单位线纵坐标。
表10.5 由n、K求6h时段单位线计算表

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




